Diagrama de Voronoi

Content
O caso mais simples
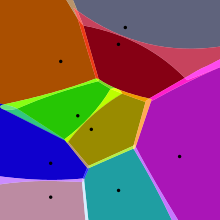
No caso mais simples, mostrado na primeira foto, recebemos um conjunto finito de pontos {p1, ..., pn} no plano euclidiano. Nesse caso, cada site PK é simplesmente um ponto, e sua célula Voronoi correspondente RK consiste em todos os pontos do plano euclidiano cuja distância para PK é menor ou igual à sua distância a qualquer outro PK. Cada uma dessas células é obtida a partir da interseção de meio espaços e, portanto, é um poliedro (convexo). Os segmentos de linha do diagrama de Voronoi são todos os pontos do avião que são equidistantes para os dois locais mais próximos. Os vértices de Voronoi (nós) são os pontos equidistantes para três (ou mais) sites.
Definição formal
Seja x {\ textStyle x} um espaço métrico com função de distância d {\ textStyle d}. Seja k {\ textstyle k} um conjunto de índices e deixe (p k) k ∈ K {\ textStyle (p_ {k}) _ {k \ in k}} ser uma tupla (coleção ordenada) de subconjuntos não vazios (o sites) no espaço x {\ textStyle x}. A célula Voronoi, ou região de Voronoi, r k {\ textstyle r_ {k}}, associada ao site p k {\ textstyle p_ {k}} é o conjunto de todos os pontos em x {\ textstyle x} a distância para p k {\ textStyle p_ {k}} não é maior que sua distância para os outros sites p j {\ textStyle p_ {j}}, onde j {\ textStyle j} é qualquer índice diferente de k {\ textstyle k}. Em outras palavras, se d (x, a) = inf {d (x, a) ∣ a ∈ A} {\ textStyle d (x, \, a) = \ inf \ {d (x, \, a) \ Mid a \ em a \}} indica a distância entre o ponto x {\ textstyle x} e o subconjunto a {\ textStyle a}, então

O diagrama Voronoi é simplesmente a tupla das células (r k) k ∈ K {\ textStyle (r_ {k}) _ {k \ in k}}. Em princípio, alguns dos sites podem se cruzar e até coincidir (um aplicativo é descrito abaixo para sites que representam lojas), mas geralmente eles são considerados descontos. Além disso, infinitamente muitos sites são permitidos na definição (essa configuração possui aplicações em geometria de números e cristalografia), mas, novamente, em muitos casos, apenas muitos sites são considerados.
No caso específico em que o espaço é um espaço euclidiano de dimensão finita, cada site é um ponto, há muitos pontos e todos são diferentes, então as células Voronoi são polítopos convexos e podem ser representados de uma maneira combinatória usando Seus vértices, lados, rostos bidimensionais, etc. Às vezes, a estrutura combinatória induzida é chamada de diagrama de Voronoi. Em geral, no entanto, as células Voronoi não podem ser convexas ou até conectadas.
No espaço euclidiano usual, podemos reescrever a definição formal em termos usuais. Cada Voronoi Polygon r K {\ textStyle r_ {k}} está associado a um ponto de gerador p k {\ textStyle p_ {k}} .Let x {\ textStyle x} seja o conjunto de todos os pontos no espaço euclidiano. Seja p 1 {\ textStyle p_ {1}} ser um ponto que gera sua região de Voronoi r 1 {\ textstyle r_ {1}}, p 2 {\ textstyle p_ {2}} que gera r 2 {\ textstyle r_ {2 {2 {2}} }} e p 3 {\ textStyle p_ {3}} que gera r 3 {\ textStyle r_ {3}} e assim por diante. Então, como expresso por Tran et al, "todos os locais no polígono Voronoi estão mais próximos do ponto do gerador desse polígono do que qualquer outro ponto de gerador no diagrama de Voronoi no plano euclidiano".
Ilustração
Como uma ilustração simples, considere um grupo de lojas em uma cidade. Suponha que queremos estimar o número de clientes de uma determinada loja. Com todo o resto sendo igual (preço, produtos, qualidade de serviço etc.), é razoável supor que os clientes escolham sua loja preferida simplesmente por considerações a distância: eles irão para a loja localizada mais próxima. Nesse caso, a célula Voronoi r k {\ displaystyle r_ {k}} de uma determinada loja p k {\ displaystyle p_ {k}} pode ser usada para fornecer uma estimativa aproximada do número de clientes em potencial que vão a esta loja (que é modelado por um ponto em nossa cidade).
Para a maioria das cidades, a distância entre os pontos pode ser medida usando a distância euclidiana familiar:
ℓ 2 = d [ ( a 1 , a 2 ) , ( b 1 , b 2 ) ] = ( a 1 − b 1 ) 2 + ( a 2 − b 2 ) 2 {\displaystyle \ell _{2}=d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]={\sqrt {\left(a_{1}-b_{1}\right)^{2}+\left(a_{2}-b_{2}\right)^{2}}}}
ou a distância de Manhattan:
d [ ( a 1 , a 2 ) , ( b 1 , b 2 ) ] = | a 1 − b 1 | + | a 2 − b 2 | {\displaystyle d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|} .
.Os diagramas de Voronoi correspondentes parecem diferentes para diferentes métricas de distância.


Propriedades
The dual graph for a Voronoi diagram (in the case of a Euclidean space with point sites) corresponds to the Delaunay triangulation for the same set of points.The closest pair of points corresponds to two adjacent cells in the Voronoi diagram.Assume the setting is the Euclidean plane and a discrete set of points is given. Then two points of the set are adjacent on the convex hull if and only if their Voronoi cells share an infinitely long side.If the space is a normed space and the distance to each site is attained (e.g., when a site is a compact set or a closed ball), then each Voronoi cell can be represented as a union of line segments emanating from the sites. As shown there, this property does not necessarily hold when the distance is not attained.Under relatively general conditions (the space is a possibly infinite-dimensional uniformly convex space, there can be infinitely many sites of a general form, etc.) Voronoi cells enjoy a certain stability property: a small change in the shapes of the sites, e.g., a change caused by some translation or distortion, yields a small change in the shape of the Voronoi cells. This is the geometric stability of Voronoi diagrams. As shown there, this property does not hold in general, even if the space is two-dimensional (but non-uniformly convex, and, in particular, non-Euclidean) and the sites are points.História e pesquisa
O uso informal dos diagramas de voronoi pode ser rastreado até Descartes em 1644. Peter Gustav Lejeune Dirichlet usou diagramas de voronoi bidimensionais e tridimensionais em seu estudo de formas quadráticas em 1850. O médico britânico John Snow usou um diagrama de 1850 para 1850. Ilustre como a maioria das pessoas que morreram no amplo surto de cólera de rua viviam mais perto da bomba de rua larga infectada do que a qualquer outra bomba de água.
Os diagramas de Voronoi têm o nome de Georgy Feodosievych Voronoy, que definiram e estudaram o caso Geral N-Dimensional em 1908. Os diagramas de Voronoi que são usados em geofísica e meteorologia para analisar os dados distribuídos espacialmente (como medições de precipitação) são chamados de Holloguns After American Metter After American Metter After American Metter After American Metter After American Menor After American Menor After American Menor After American After American Daters (como medições de precipitação) são chamados de Holloguns After Americanten After American Metter depois . Thiessen. Outros nomes equivalentes para esse conceito (ou casos específicos importantes): Voronoi Polyhedra, polígonos de Voronoi, domínio (s) de influência, decomposição de Voronoi, tesellation (s) de Voronoi, tesellation (s) de Dirichlet.
Exemplos

As teselações de Voronoi de treliças regulares de pontos em duas ou três dimensões dão origem a muitos biblioadianas familiares.
A 2D lattice gives an irregular honeycomb tessellation, with equal hexagons with point symmetry; in the case of a regular triangular lattice it is regular; in the case of a rectangular lattice the hexagons reduce to rectangles in rows and columns; a square lattice gives the regular tessellation of squares; note that the rectangles and the squares can also be generated by other lattices (for example the lattice defined by the vectors (1,0) and (1/2,1/2) gives squares).A simple cubic lattice gives the cubic honeycomb.A hexagonal close-packed lattice gives a tessellation of space with trapezo-rhombic dodecahedra.A face-centred cubic lattice gives a tessellation of space with rhombic dodecahedra.A body-centred cubic lattice gives a tessellation of space with truncated octahedra.Parallel planes with regular triangular lattices aligned with each other's centers give the hexagonal prismatic honeycomb.Certain body-centered tetragonal lattices give a tessellation of space with rhombo-hexagonal dodecahedra.Para o conjunto de pontos (x, y) com x em um conjunto discreto x e y em um conjunto discreto Y, obtemos telhas retangulares com os pontos não necessariamente em seus centros.
Diagramas Voronoi de ordem superior
Embora uma célula voronoi normal seja definida como o conjunto de pontos mais próximos de um único ponto em S, uma célula Voronoi de Nth-Ordem é definida como o conjunto de pontos com um conjunto específico de n pontos em S como seus n vizinhos mais próximos. Os diagramas Voronoi de ordem superior também subdividem o espaço.
Os diagramas de voronoi de ordem superior podem ser gerados recursivamente. Para gerar o diagrama Voronoi da Nth-Ordem a partir do conjunto S, comece com o diagrama de ordem TH (n-1) e substitua cada célula gerada por x = {x1, x2, ..., xn-1} com um diagrama de voronoi gerado No conjunto S - X.
Diagrama Voronoi mais distante do ponto
Para um conjunto de n pontos, o diagrama Voronoi (n-1) de ordem TH é chamado de diagrama Voronoi mais distante.
Para um determinado conjunto de pontos s = {p1, p2, ..., pn} o diagrama Voronoi mais distante divide o plano em células nas quais o mesmo ponto de p é o ponto mais distante. Um ponto de p tem uma célula no diagrama Voronoi mais distante de ponto se e somente se for um vértice do casco convexo de P. Seja h = {h1, h2, ..., hk} seja o casco convexo de p; Então, o diagrama Voronoi mais distante é uma subdivisão do plano nas células K, uma para cada ponto em H, com a propriedade de que um ponto q está na célula correspondente a um local hi se e somente se d (q, oi) > d (q, pj) para cada pj ∈ S com hi ≠ pj, onde d (p, q) é a distância euclidiana entre dois pontos p e q.
Os limites das células no diagrama Voronoi mais distante têm a estrutura de uma árvore topológica, com raios infinitos como folhas. Toda árvore finita é isomórfica da árvore formada dessa maneira a partir de um diagrama Voronoi mais distante.
Generalizações e variações
Conforme implícito na definição, as células Voronoi podem ser definidas para métricas que não sejam euclidianas, como a distância Mahalanobis ou a distância de Manhattan. No entanto, nesses casos, os limites das células Voronoi podem ser mais complicados do que no caso euclidiano, uma vez que o locus equidistante por dois pontos pode deixar de ser subespaço da codimensão 1, mesmo no caso bidimensional.
Um diagrama de Voronoi ponderado é aquele em que a função de um par de pontos para definir uma célula Voronoi é uma função de distância modificada por pesos multiplicativos ou aditivos atribuídos aos pontos do gerador. Em contraste com o caso de células Voronoi definidas usando uma distância que é uma métrica, neste caso algumas das células Voronoi podem estar vazias. Um diagrama de energia é um tipo de diagrama de voronoi definido a partir de um conjunto de círculos usando a distância de potência; Também pode ser pensado como um diagrama de voronoi ponderado, no qual um peso definido a partir do raio de cada círculo é adicionado à distância euclidiana quadrada do centro do círculo.
O diagrama Voronoi de n {\ displayStyle n} aponta em d {\ displayStyle d} -o espaço dimensional pode ter o (n ⌈ d / 2 ⌉) {\ textstyle o (n^{\ lceil d / 2 \ rceil})} vértices, exigindo o mesmo limite para a quantidade de memória necessária para armazenar uma descrição explícita dela. Portanto, os diagramas de voronoi geralmente não são viáveis para dimensões moderadas ou altas. Uma alternativa mais eficiente em termos espaciais é usar diagramas de voronoi aproximados.
Os diagramas de voronoi também estão relacionados a outras estruturas geométricas, como o eixo medial (que encontrou aplicações na segmentação de imagens, reconhecimento de caracteres ópticos e outras aplicações computacionais), esqueleto reto e diagramas de zona.
Formulários
Meteorologia/hidrologia
É usado na hidrologia de meteorologia e engenharia para encontrar os pesos para dados de precipitação das estações em uma área (bacia hidrográfica). Os pontos que geram os polígonos são a várias estação que registram dados de precipitação. Os bissetores perpendiculares são atraídos para a linha que une duas estações. Isso resulta na formação de polígonos ao redor das estações. A área (a i) {\ DisplayStyle (a_ {i})} O ponto da estação de toque é conhecido como área de influência da estação. A precipitação média é calculada pela fórmula p ¯ = ∑ a i p i ∑ a i {\ displayStyle {\ bar {p}} = {\ frac {\ sum a_ {i} p_ {i}} {\ sum a_ { eu}}}}
Humanidades
In classical archaeology, specifically art history, the symmetry of statue heads is analyzed to determine the type of statue a severed head may have belonged to. An example of this that made use of Voronoi cells was the identification of the Sabouroff head, which made use of a high-resolution polygon mesh.In dialectometry, Voronoi cells are used to indicate a supposed linguistic continuity between survey points.Ciências Naturais

Saúde
In medical diagnosis, models of muscle tissue, based on Voronoi diagrams, can be used to detect neuromuscular diseases.In epidemiology, Voronoi diagrams can be used to correlate sources of infections in epidemics. One of the early applications of Voronoi diagrams was implemented by John Snow to study the 1854 Broad Street cholera outbreak in Soho, England. He showed the correlation between residential areas on the map of Central London whose residents had been using a specific water pump, and the areas with the most deaths due to the outbreak.Engenharia
In polymer physics, Voronoi diagrams can be used to represent free volumes of polymers.In materials science, polycrystalline microstructures in metallic alloys are commonly represented using Voronoi tessellations. In island growth, the Voronoi diagram is used to estimate the growth rate of individual islands. In solid-state physics, the Wigner-Seitz cell is the Voronoi tessellation of a solid, and the Brillouin zone is the Voronoi tessellation of reciprocal (wavenumber) space of crystals which have the symmetry of a space group.In aviation, Voronoi diagrams are superimposed on oceanic plotting charts to identify the nearest airfield for in-flight diversion (see ETOPS), as an aircraft progresses through its flight plan.In architecture, Voronoi patterns were the basis for the winning entry for the redevelopment of The Arts Centre Gold Coast.In urban planning, Voronoi diagrams can be used to evaluate the Freight Loading Zone system.In mining, Voronoi polygons are used to estimate the reserves of valuable materials, minerals, or other resources. Exploratory drillholes are used as the set of points in the Voronoi polygons.In surface metrology, Voronoi tessellation can be used for surface roughness modeling.In robotics, some of the control strategies and path planning algorithms of multi-robot systems are based on the Voronoi partitioning of the environment.Geometria
A point location data structure can be built on top of the Voronoi diagram in order to answer nearest neighbor queries, where one wants to find the object that is closest to a given query point. Nearest neighbor queries have numerous applications. For example, one might want to find the nearest hospital or the most similar object in a database. A large application is vector quantization, commonly used in data compression.In geometry, Voronoi diagrams can be used to find the largest empty circle amid a set of points, and in an enclosing polygon; e.g. to build a new supermarket as far as possible from all the existing ones, lying in a certain city.Voronoi diagrams together with farthest-point Voronoi diagrams are used for efficient algorithms to compute the roundness of a set of points. The Voronoi approach is also put to use in the evaluation of circularity/roundness while assessing the dataset from a coordinate-measuring machine.Informática
In networking, Voronoi diagrams can be used in derivations of the capacity of a wireless network.In computer graphics, Voronoi diagrams are used to calculate 3D shattering / fracturing geometry patterns. It is also used to procedurally generate organic or lava-looking textures.In autonomous robot navigation, Voronoi diagrams are used to find clear routes. If the points are obstacles, then the edges of the graph will be the routes furthest from obstacles (and theoretically any collisions).In machine learning, Voronoi diagrams are used to do 1-NN classifications.In global scene reconstruction, including with random sensor sites and unsteady wake flow, geophysical data, and 3D turbulence data, Voronoi tesselations are used with deep learning.In user interface development, Voronoi patterns can be used to compute the best hover state for a given point.Civics e planejamento
In Melbourne, government school students are always eligible to attend the nearest primary school or high school to where they live, as measured by a straight-line distance. The map of school zones is therefore a Voronoi diagram.Padaria
Ukrainian Pastry chef Dinara Kasko uses the mathematical principles of the Voronoi diagram to create silicone molds made with a 3D printer to shape her original cakes.Algoritmos
Vários algoritmos eficientes são conhecidos por construir diagramas de voronoi, diretamente (como o próprio diagrama) ou indiretamente, começando com uma triangulação de Delaunay e depois obtendo seu duplo. Um diagrama de voronoi de um conjunto de pontos em um algoritmo de avião. Para o diagrama de Voronoi. O algoritmo de inundação de salto pode gerar diagramas aproximados de voronoi em tempo constante e é adequado para uso no hardware gráfico de commodity.
O algoritmo de Lloyd e sua generalização através do algoritmo Linde-Buzo-Gray (AKA K-Means agrupando), use a construção de diagramas de voronoi como um sub-rotina. Esses métodos alternam entre as etapas em que se constrói o diagrama de voroni para um conjunto de pontos de semente, e etapas nas quais os pontos de sementes são movidos para novos locais mais centrais em suas células. Esses métodos podem ser usados em espaços de dimensão arbitrária para convergir iterativamente em direção a uma forma especializada do diagrama de Voronoi, chamado de teselação de Voronoi centróide, onde os locais foram movidos para pontos que também são os centros geométricos de suas células.






