Latitude

Content
Fundo
Dois níveis de abstração são empregados nas definições de latitude e longitude. Na primeira etapa, a superfície física é modelada pela geóide, uma superfície que se aproxima do nível médio do mar sobre os oceanos e sua continuação sob as massas terrestres. A segunda etapa é aproximar o geóide por uma superfície de referência matematicamente mais simples. A escolha mais simples para a superfície de referência é uma esfera, mas o geóide é modelado com mais precisão por um elipsóide. As definições de latitude e longitude nessas superfícies de referência são detalhadas nas seções a seguir. Linhas de latitude e longitude constantes constituem uma gratícula na superfície de referência. A latitude de um ponto na superfície real é a do ponto correspondente na superfície de referência, sendo a correspondência ao longo do normal à superfície de referência, que passa pelo ponto na superfície física. A latitude e a longitude, juntamente com alguma especificação de altura, constituem um sistema de coordenadas geográficas, conforme definido na especificação do padrão ISO 19111.
Como existem muitos elipsóides de referência diferentes, a latitude precisa de uma característica na superfície não é única: isso é estressado no padrão ISO, que afirma que "sem a especificação completa do sistema de referência de coordenadas, coordenadas (que é latitude e longitude) são ambíguos na melhor das hipóteses e sem sentido na pior das hipóteses ". Isso é de grande importância em aplicações precisas, como um sistema de posicionamento global (GPS), mas em uso comum, onde não é necessária alta precisão, o elipsóide de referência geralmente não é declarado.
Nos textos em inglês, o ângulo de latitude, definido abaixo, geralmente é indicado pela letra de caso inferior grega Phi (ϕ ou φ). É medido em graus, minutos e segundos ou graus decimais, norte ou sul do equador. Para fins de navegação, as posições são apresentadas em graus e minutos decimais. Por exemplo, o farol de agulhas está a 50 ° 39.734 ′ N 001 ° 35.500 ′ W.
Este artigo refere -se a coordenar sistemas para a Terra: pode ser adaptado para cobrir a lua, planetas e outros objetos celestes (latitude planetográfica).
Para uma breve história, veja História da Latitude.
Determinação
Na navegação celestial, a latitude é determinada com o método da altitude meridiana. Mais uma medição precisa da latitude requer uma compreensão do campo gravitacional da Terra, para configurar teodolitos ou determinar as órbitas de satélite GPS. O estudo da figura da Terra, juntamente com seu campo gravitacional, é a ciência da geodesia.
Latitude na esfera
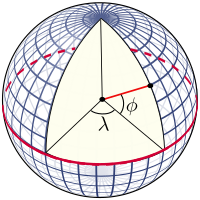
 ) and longitude ( λ {\displaystyle \lambda }
) and longitude ( λ {\displaystyle \lambda }  ) are defined on a spherical model. The graticule spacing is 10 degrees.
) are defined on a spherical model. The graticule spacing is 10 degrees.A gratula na esfera
A grática é formada pelas linhas de latitude constante e longitude constante, que são construídas com referência ao eixo de rotação da terra. Os principais pontos de referência são os pólos onde o eixo de rotação da Terra cruza a superfície de referência. Os aviões que contêm o eixo de rotação cruzam a superfície nos meridianos; e o ângulo entre qualquer plano meridiano e que através de Greenwich (o Meridiano Prime) define a longitude: os meridianos são linhas de longitude constante. O plano através do centro da terra e perpendicular ao eixo de rotação cruza a superfície em um grande círculo chamado Equador. Planos paralelos ao plano equatorial cruzam a superfície em círculos de latitude constante; Estes são os paralelos. O equador tem uma latitude de 0 °, o pólo norte tem uma latitude de 90 ° norte (escrito 90 ° N ou +90 °) e o pólo sul tem uma latitude de 90 ° sul (escrito 90 ° S ou -90 ° ). A latitude de um ponto arbitrário é o ângulo entre o plano equatorial e o normal à superfície nesse ponto: o normal à superfície da esfera está ao longo do vetor radial.
A latitude, conforme definida dessa maneira para a esfera, é frequentemente denominada latitude esférica, para evitar a ambiguidade com a latitude geodética e as latitudes auxiliares definidas nas seções subsequentes deste artigo.
Nomeadas latitudes na terra
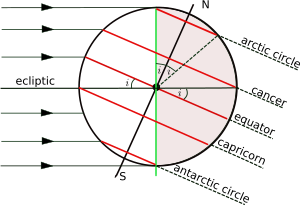
Além do equador, outros quatro paralelos são importantes:
Arctic Circle66° 34′ (66.57°) NTropic of Cancer23° 26′ (23.43°) NTropic of Capricorn23° 26′ (23.43°) SAntarctic Circle66° 34′ (66.57°) SO plano da órbita da Terra sobre o Sol é chamado de eclíptica, e o plano perpendicular ao eixo de rotação da terra é o plano equatorial. O ângulo entre a eclíptica e o plano equatorial é chamado de uma inclinação axial, a obliquidade ou a inclinação do eclíptico, e é convencionalmente denotada por i. A latitude dos círculos tropicais é igual a I e a latitude dos círculos polares é o seu complemento (90 ° - I). O eixo de rotação varia lentamente ao longo do tempo e os valores apresentados aqui são os da época atual. A variação de tempo é discutida mais detalhadamente no artigo sobre inclinação axial.
A figura mostra a geometria de uma seção transversal do plano perpendicular à eclíptica e através dos centros da terra e do sol no solstício de dezembro, quando o sol está no alto em algum ponto do tropical de Capricórnio. As latitudes polares sul abaixo do círculo antártico estão à luz do dia, enquanto as latitudes polares do norte acima do círculo ártico estão à noite. A situação é revertida no solstício de junho, quando o sol está no topo do trópico de câncer. Somente em latitudes entre os dois trópicos é possível que o sol esteja diretamente no alto (no zênite).
Nas projeções de mapa, não existe uma regra universal sobre como os meridianos e paralelos devem aparecer. Os exemplos abaixo mostram os paralelos nomeados (como linhas vermelhas) na projeção Mercator comumente usada e na projeção transversal do Mercator. No primeiro, os paralelos são horizontais e os meridianos são verticais, enquanto que no último não há relação exata de paralelos e meridianos com horizontal e vertical: ambos são curvas complicadas.
Normal MercatorTransverse Mercator
\

Latitude no elipsóide
Elipsóides
Em 1687, Isaac Newton publicou o Philosophiæ Naturalis Principia Mathematica, no qual provou que um corpo fluido auto-gravado rotativo em equilíbrio assume a forma de um elipsóide oblato. (Este artigo usa o termo elipsóide em preferência ao esferóide mais antigo.) O resultado de Newton foi confirmado por medições geodésicas no século XVIII. (Ver Arc.) Um elipsóide oblato é a superfície tridimensional gerada pela rotação de uma elipse em torno de seu eixo mais curto (eixo menor). "Elipsóide oblato da revolução" é abreviado para "elipsóides" no restante deste artigo. (Os elipsóides que não têm um eixo de simetria são denominados triaxiais.)
Muitos elipsóides de referência diferentes foram usados na história da geodesia. Nos dias pré-satélite, eles foram criados para dar um bom ajuste ao geoid sobre a área limitada de uma pesquisa, mas, com o advento do GPS, tornou-se natural usar elipsóides de referência (como WGS84) com o centro no centro de massa da terra e eixo menor alinhado ao eixo de rotação da terra. Esses elipsóides geocêntricos geralmente estão a 100 m (330 pés) do geoid. Como a latitude é definida em relação a um elipsóide, a posição de um determinado ponto é diferente em cada elipsóide: não se pode especificar exatamente a latitude e a longitude de um recurso geográfico sem especificar o elipsóide usado. Muitos mapas mantidos pelas agências nacionais são baseados em elipsóides mais antigos; portanto, é preciso saber como os valores de latitude e longitude são transformados de um elipsóide para outro. Os aparelhos GPS incluem software para realizar transformações de dado que vinculam o WGS84 ao elipsóide de referência local à sua grade associada.
A geometria do elipsóide

A forma de um elipsóide da revolução é determinada pela forma da elipse que é girada em torno de seu eixo menor (mais curto). Dois parâmetros são necessários. Um é invariavelmente o raio equatorial, que é o eixo semi-major, a. O outro parâmetro é geralmente (1) o raio polar ou o eixo semi-minor, b; ou (2) o (primeiro) achatamento, f; ou (3) a excentricidade, e. Esses parâmetros não são independentes: eles são relacionados por
f = a − b a , e 2 = 2 f − f 2 , b = a ( 1 − f ) = a 1 − e 2 . {\displaystyle f={\frac {a-b}{a}},\qquad e^{2}=2f-f^{2},\qquad b=a(1-f)=a{\sqrt {1-e^{2}}}\,.}
Muitos outros parâmetros (ver Ellipse, Ellipsoid) aparecem no estudo das projeções de geodesia, geofísica e mapa, mas todos podem ser expressos em termos de um ou dois membros do conjunto A, B, F e E. Ambos F e E são pequenos e geralmente aparecem em expansões em série em cálculos; Eles são da ordem 1/298 e 0,0818, respectivamente. Os valores para vários elipsóides são apresentados na figura da Terra. Os elipsóides de referência são geralmente definidos pelo eixo semi-major e pelo achatamento inverso, 1/f. Por exemplo, os valores definidores para o elipsóide WGS84, usados por todos os dispositivos GPS, são
a (equatorial radius): 6378137.0 m exactly1/f (inverse flattening): 298.257223563 exactlydos quais são derivados
b (polar radius): 6356752.31425 me2 (eccentricity squared): 0.00669437999014A diferença entre os eixos semi-major e semi-minor é de cerca de 21 km (13 milhas) e, como a fração do eixo semi-major, é igual ao achatamento; Em um monitor de computador, o elipsóide pode ser dimensionado como 300 por 299 pixels. Isso mal seria distinguível de uma esfera de 300 por 300 pixels, então as ilustrações geralmente exageram o achatamento.
Latitudes geodésicas e geocêntricas

 ) and longitude ( λ {\displaystyle \lambda }
) and longitude ( λ {\displaystyle \lambda }  ) on an ellipsoid. The normal to the surface does not pass through the centre, except at the equator and at the poles.
) on an ellipsoid. The normal to the surface does not pass through the centre, except at the equator and at the poles.A grática no elipsóide é construída exatamente da mesma maneira que na esfera. O normal em um ponto na superfície de um elipsóide não passa pelo centro, exceto para pontos no equador ou nos pólos, mas a definição de latitude permanece inalterada como o ângulo entre o plano normal e o equatorial. A terminologia para latitude deve ser mais precisa, distinguindo:
Geodetic latitude: the angle between the normal and the equatorial plane. The standard notation in English publications is ϕ. This is the definition assumed when the word latitude is used without qualification. The definition must be accompanied with a specification of the ellipsoid.Geocentric latitude (also known as spherical latitude, after the 3D polar angle): the angle between the radius (from centre to the point on the surface) and the equatorial plane. (Figure below). There is no standard notation: examples from various texts include θ, ψ, q, ϕ′, ϕc, ϕg. This article uses θ.A latitude geográfica deve ser usada com cuidado, pois alguns autores o usam como sinônimo de latitude geodésica, enquanto outros o usam como uma alternativa à latitude astronômica. "Latitude" (não qualificada) deve normalmente se referir à latitude geodética.
A importância de especificar o dado de referência pode ser ilustrada por um exemplo simples. No elipsóide de referência para WGS84, o centro da Torre Eiffel possui uma latitude geodésica de 48 ° 51 ′ 29 ″ N, ou 48.8583 ° N e longitude de 2 ° 17 ′ 40 ″ E ou 2.2944 ° E. As mesmas coordenadas no dado ED50 definem um ponto no solo, que fica a 140 metros (460 pés) distante da torre. [Citação necessária] Uma pesquisa na web pode produzir vários valores diferentes para a latitude da torre; O elipsóide de referência raramente é especificado.
Distância meridiana
O comprimento de um grau de latitude depende da figura da terra assumida.
Distância meridiana na esfera
Na esfera, o normal passa pelo centro e a latitude (ϕ) é antes igual ao ângulo subtendido no centro pelo arco meridiano do equador até o ponto em questão. Se a distância meridiana for indicada por m (ϕ) então
m ( ϕ ) = π 180 ∘ R ϕ d e g r e e s = R ϕ r a d i a n s {\displaystyle m(\phi )={\frac {\pi }{180^{\circ }}}R\phi _{\mathrm {degrees} }=R\phi _{\mathrm {radians} }}
onde R denota o raio médio da terra. R é igual a 6.371 km ou 3.959 milhas. Nenhuma precisão mais alta é apropriada para r, pois os resultados de maior precisão exigem um modelo elipsóide. Com esse valor para r, o comprimento meridiano de 1 grau de latitude na esfera é de 111,2 km (69,1 milhas estatutárias) (60,0 milhas náuticas). O comprimento de 1 minuto de latitude é de 1,853 km (1,151 milhas estatutárias) (1,00 milhas náuticas), enquanto o comprimento de 1 segundo de latitude é de 30,8 m ou 101 pés (ver milha náutica).
Distância meridiana no elipsóide
No arco meridiano e textos padrão, é mostrado que a distância ao longo de um meridiano da latitude ϕ ao equador é dada por (ϕ em radianos)
m ( ϕ ) = ∫ 0 ϕ M ( ϕ ′ ) d ϕ ′ = a ( 1 − e 2 ) ∫ 0 ϕ ( 1 − e 2 sin 2 ϕ ′ ) − 3 2 d ϕ ′ {\displaystyle m(\phi )=\int _{0}^{\phi }M(\phi ')\,d\phi '=a\left(1-e^{2}\right)\int _{0}^{\phi }\left(1-e^{2}\sin ^{2}\phi '\right)^{-{\frac {3}{2}}}\,d\phi '}
onde m (ϕ) é o raio meridional de curvatura.
A distância meridiana do trimestre do equador para o poste é
m p = m ( π 2 ) {\displaystyle m_{\mathrm {p} }=m\left({\frac {\pi }{2}}\right)\,}
Para WGS84, essa distância é de 10001.965729 km.
A avaliação da distância do meridiano é central para muitos estudos em geodesia e projeção de mapas. Ele pode ser avaliado expandindo a integral pela série binomial e integrando o termo por termo: consulte o Meridian ARC para obter detalhes. O comprimento do arco meridiano entre duas latitudes é dado substituindo os limites da integral pelas latitudes em questão. O comprimento de um pequeno arco meridiano é dado por
δ m ( ϕ ) = M ( ϕ ) δ ϕ = a ( 1 − e 2 ) ( 1 − e 2 sin 2 ϕ ) − 3 2 δ ϕ {\displaystyle \delta m(\phi )=M(\phi )\,\delta \phi =a\left(1-e^{2}\right)\left(1-e^{2}\sin ^{2}\phi \right)^{-{\frac {3}{2}}}\,\delta \phi } ϕ {\displaystyle \phi }
ϕ {\displaystyle \phi }  Δ1latΔ1long0°110.574 km111.320 km15°110.649 km107.550 km30°110.852 km96.486 km45°111.132 km78.847 km60°111.412 km55.800 km75°111.618 km28.902 km90°111.694 km0.000 km
Δ1latΔ1long0°110.574 km111.320 km15°110.649 km107.550 km30°110.852 km96.486 km45°111.132 km78.847 km60°111.412 km55.800 km75°111.618 km28.902 km90°111.694 km0.000 kmQuando a diferença de latitude é de 1 grau, correspondente a π/180 radianos, a distância do arco é sobre
Δ lat 1 = π a ( 1 − e 2 ) 180 ∘ ( 1 − e 2 sin 2 ϕ ) 3 2 {\displaystyle \Delta _{\text{lat}}^{1}={\frac {\pi a\left(1-e^{2}\right)}{180^{\circ }\left(1-e^{2}\sin ^{2}\phi \right)^{\frac {3}{2}}}}}
A distância nos metros (correta a 0,01 metro) entre as latitudes ϕ {\ displaystyle \ phi} - 0,5 graus e ϕ {\ displaystyle \ phi} + 0,5 graus no esferóide WGS84 Is
Δ lat 1 = 111 132.954 − 559.822 cos 2 ϕ + 1.175 cos 4 ϕ {\displaystyle \Delta _{\text{lat}}^{1}=111\,132.954-559.822\cos 2\phi +1.175\cos 4\phi }
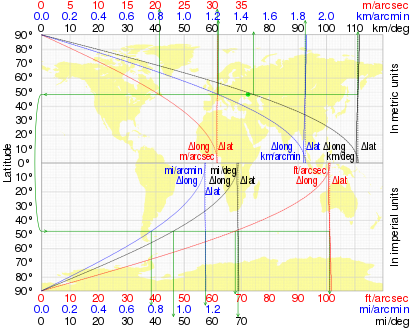
A variação dessa distância com a latitude (no WGS84) é mostrada na tabela junto com o comprimento de um grau de longitude (distância leste -oeste):
Δ long 1 = π a cos ϕ 180 ∘ 1 − e 2 sin 2 ϕ {\displaystyle \Delta _{\text{long}}^{1}={\frac {\pi a\cos \phi }{180^{\circ }{\sqrt {1-e^{2}\sin ^{2}\phi }}}}\,}
Uma calculadora para qualquer latitude é fornecida pela Agência Nacional de Inteligência Geoespacial do governo dos EUA (NGA).
O gráfico a seguir ilustra a variação de um grau de latitude e um grau de longitude com latitude.
Latitudes auxiliares
Existem seis latitudes auxiliares que têm aplicações para problemas especiais em geodesia, geofísica e a teoria das projeções de mapa:
Geocentric latitudeParametric (or reduced) latitudeRectifying latitudeAuthalic latitudeConformal latitudeIsometric latitudeAs definições fornecidas nesta seção estão relacionadas a locais no elipsóide de referência, mas as duas primeiras latitudes auxiliares, como a latitude geodética, podem ser estendidas para definir um sistema de coordenadas geográficas tridimensionais, conforme discutido abaixo. As latitudes restantes não são usadas dessa maneira; Eles são usados apenas como construções intermediárias nas projeções de mapa do elipsóide de referência para o plano ou nos cálculos da geodésica no elipsóide. Seus valores numéricos não são de interesse. Por exemplo, ninguém precisaria calcular a latitude autálica da Torre Eiffel.
As expressões abaixo dão as latitudes auxiliares em termos de latitude geodética, o eixo semi-major, a e a excentricidade, e. (Para os inversos, veja abaixo.) Os formulários fornecidos são, além das variantes notacionais, aquelas na referência padrão para projeções de mapa, "projeções de mapa: um manual de trabalho", de J. P. Snyder. As derivações dessas expressões podem ser encontradas em Adams e publicações on -line de Osborne e Rapp.
Latitude geocêntrica

A latitude geocêntrica é o ângulo entre o plano equatorial e o raio do centro para um ponto de interesse.
Quando o ponto está na superfície do elipsóide, a relação entre a latitude geocêntrica (θ) e a latitude geodética (ϕ) é:
θ ( ϕ ) = tan − 1 ( ( 1 − e 2 ) tan ϕ ) = tan − 1 ( ( 1 − f ) 2 tan ϕ ) . {\displaystyle \theta (\phi )=\tan ^{-1}\left(\left(1-e^{2}\right)\tan \phi \right)=\tan ^{-1}\left((1-f)^{2}\tan \phi \right)\,.}
Para pontos que não estão na superfície do elipsóide, o relacionamento envolve adicionalmente a altura elipsoidal h:
θ ( ϕ , h ) = tan − 1 ( N ( 1 − f ) 2 + h N + h tan ϕ ) {\displaystyle \theta (\phi ,h)=\tan ^{-1}\left({\frac {N(1-f)^{2}+h}{N+h}}\tan \phi \right)}
As latitudes geodésicas e geocêntricas são iguais no equador e nos pólos, mas em outras latitudes diferem em alguns minutos de arco. Tomando o valor da excentricidade ao quadrado como 0,0067 (depende da escolha do elipsóide) a diferença máxima de ϕ-θ {\ displaystyle \ phi {-} \ theta} de aproximadamente 45 ° 6 ′.
Latitude paramétrica (ou latitude reduzida)

A latitude paramétrica ou a latitude reduzida, β, é definida pelo raio extraído do centro do elipsóide para esse ponto q na esfera circundante (do raio A), que é a projeção paralela ao eixo da Terra de um ponto P no elipsóide na latitude ϕ. Foi introduzido por Legendre e Bessel, que resolveu problemas para geodésicos no elipsóide, transformando -os em um problema equivalente para a geodésica esférica usando essa menor latitude. A notação de Bessel, U (ϕ), também é usada na literatura atual. A latitude paramétrica está relacionada à latitude geodésica por:
β ( ϕ ) = tan − 1 ( 1 − e 2 tan ϕ ) = tan − 1 ( ( 1 − f ) tan ϕ ) {\displaystyle \beta (\phi )=\tan ^{-1}\left({\sqrt {1-e^{2}}}\tan \phi \right)=\tan ^{-1}\left((1-f)\tan \phi \right)}
O nome alternativo surge da parametrização da equação da elipse descrevendo uma seção meridiana. Em termos de coordenadas cartesianas P, a distância do eixo menor e Z, a distância acima do plano equatorial, a equação da elipse é:
p 2 a 2 + z 2 b 2 = 1 . {\displaystyle {\frac {p^{2}}{a^{2}}}+{\frac {z^{2}}{b^{2}}}=1\,.}
As coordenadas cartesianas do ponto são parametrizadas por
p = a cos β , z = b sin β ; {\displaystyle p=a\cos \beta \,,\qquad z=b\sin \beta \,;}
Cayley sugeriu o termo latitude paramétrica devido à forma dessas equações.
A latitude paramétrica não é usada na teoria das projeções de mapa. Sua aplicação mais importante está na teoria da geodésica elipsóide (Vincenty, Karney).
Latitude retificadora
A latitude retificadora, μ, é a distância meridiana escalada para que seu valor nos pólos seja igual a 90 graus ou radianos π/2:
μ ( ϕ ) = π 2 m ( ϕ ) m p {\displaystyle \mu (\phi )={\frac {\pi }{2}}{\frac {m(\phi )}{m_{\mathrm {p} }}}}
onde a distância meridiana do equador para uma latitude ϕ é (ver arco meridiano)
m ( ϕ ) = a ( 1 − e 2 ) ∫ 0 ϕ ( 1 − e 2 sin 2 ϕ ′ ) − 3 2 d ϕ ′ , {\displaystyle m(\phi )=a\left(1-e^{2}\right)\int _{0}^{\phi }\left(1-e^{2}\sin ^{2}\phi '\right)^{-{\frac {3}{2}}}\,d\phi '\,,}
e o comprimento do quadrante meridiano do equador para o pólo (a distância polar) é
m p = m ( π 2 ) . {\displaystyle m_{\mathrm {p} }=m\left({\frac {\pi }{2}}\right)\,.}
Usando a latitude retificadora para definir uma latitude em uma esfera de raio
R = 2 m p π {\displaystyle R={\frac {2m_{\mathrm {p} }}{\pi }}}
Define uma projeção do elipsóide para a esfera, de modo que todos os meridianos tenham um comprimento e escala uniforme verdadeiros. A esfera pode então ser projetada para o avião com uma projeção equirectangular para dar uma dupla projeção do elipsóide ao avião, de modo que todos os meridianos tenham um comprimento verdadeiro e escala meridiana uniforme. Um exemplo do uso da latitude retificadora é a projeção cônica equidistante. (Snyder, Seção 16). A latitude retificadora também é de grande importância na construção da projeção transversal do Mercator.
Latitude autálica
A latitude autálica (após o grego para a "mesma área"), ξ, fornece uma transformação de preservação de área em uma esfera.
ξ ( ϕ ) = sin − 1 ( q ( ϕ ) q p ) {\displaystyle \xi (\phi )=\sin ^{-1}\left({\frac {q(\phi )}{q_{\mathrm {p} }}}\right)}
Onde
q ( ϕ ) = ( 1 − e 2 ) sin ϕ 1 − e 2 sin 2 ϕ − 1 − e 2 2 e ln ( 1 − e sin ϕ 1 + e sin ϕ ) = ( 1 − e 2 ) sin ϕ 1 − e 2 sin 2 ϕ + 1 − e 2 e tanh − 1 ( e sin ϕ ) {\displaystyle {\begin{aligned}q(\phi )&={\frac {\left(1-e^{2}\right)\sin \phi }{1-e^{2}\sin ^{2}\phi }}-{\frac {1-e^{2}}{2e}}\ln \left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)\\[2pt]&={\frac {\left(1-e^{2}\right)\sin \phi }{1-e^{2}\sin ^{2}\phi }}+{\frac {1-e^{2}}{e}}\tanh ^{-1}(e\sin \phi )\end{aligned}}}
e
q p = q ( π 2 ) = 1 − 1 − e 2 2 e ln ( 1 − e 1 + e ) = 1 + 1 − e 2 e tanh − 1 e {\displaystyle {\begin{aligned}q_{\mathrm {p} }=q\left({\frac {\pi }{2}}\right)&=1-{\frac {1-e^{2}}{2e}}\ln \left({\frac {1-e}{1+e}}\right)\\&=1+{\frac {1-e^{2}}{e}}\tanh ^{-1}e\end{aligned}}}
e o raio da esfera é tomado como
R q = a q p 2 . {\displaystyle R_{q}=a{\sqrt {\frac {q_{\mathrm {p} }}{2}}}\,.}
Um exemplo do uso da latitude autálica é a projeção cônica da área igual.
Latitude conforme
A latitude conforme, χ, fornece uma transformação de preservação de ângulo (conforme) na esfera.
χ ( ϕ ) = 2 tan − 1 [ ( 1 + sin ϕ 1 − sin ϕ ) ( 1 − e sin ϕ 1 + e sin ϕ ) e ] 1 2 − π 2 = 2 tan − 1 [ tan ( ϕ 2 + π 4 ) ( 1 − e sin ϕ 1 + e sin ϕ ) e 2 ] − π 2 = tan − 1 [ sinh ( sinh − 1 ( tan ϕ ) − e tanh − 1 ( e sin ϕ ) ) ] = gd [ gd − 1 ( ϕ ) − e tanh − 1 ( e sin ϕ ) ] {\displaystyle {\begin{aligned}\chi (\phi )&=2\tan ^{-1}\left[\left({\frac {1+\sin \phi }{1-\sin \phi }}\right)\left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)^{e}\right]^{\frac {1}{2}}-{\frac {\pi }{2}}\\[2pt]&=2\tan ^{-1}\left[\tan \left({\frac {\phi }{2}}+{\frac {\pi }{4}}\right)\left({\frac {1-e\sin \phi }{1+e\sin \phi }}\right)^{\frac {e}{2}}\right]-{\frac {\pi }{2}}\\[2pt]&=\tan ^{-1}\left[\sinh \left(\sinh ^{-1}(\tan \phi )-e\tanh ^{-1}(e\sin \phi )\right)\right]\\&=\operatorname {gd} \left[\operatorname {gd} ^{-1}(\phi )-e\tanh ^{-1}(e\sin \phi )\right]\end{aligned}}}
onde GD (x) é a função Gudermannian. (Veja também projeção Mercator.)
A latitude conforme define uma transformação do elipsóide em uma esfera de raio arbitrário, de modo que o ângulo de interseção entre duas linhas no elipsóide seja o mesmo que o ângulo correspondente na esfera (para que a forma de pequenos elementos seja bem preservada) . Outra transformação conforme da esfera para o plano fornece uma projeção dupla conforme do elipsóide para o plano. Esta não é a única maneira de gerar uma projeção tão conforme. Por exemplo, a versão 'exata' da projeção transversal do Mercator no elipsóide não é uma projeção dupla. (No entanto, envolve uma generalização da latitude conforme para o plano complexo).
Latitude isométrica
A latitude isométrica, ψ, é usada no desenvolvimento das versões elipsoidais da projeção normal do Mercator e da projeção transversal do Mercator. O nome "isométrico" surge do fato de que, em qualquer ponto do elipsóide, incrementos iguais de ψ e longitude λ dão origem a deslocamentos de distância igual ao longo dos meridianos e paralelos, respectivamente. A gratícula definida pelas linhas de constante ψ e constante λ, divide a superfície do elipsóide em uma malha de quadrados (de tamanho variável). A latitude isométrica é zero no equador, mas diverge rapidamente da latitude geodética, tendendo ao infinito nos pólos. A notação convencional é dada em Snyder (página 15):
ψ ( ϕ ) = ln [ tan ( π 4 + ϕ 2 ) ] + e 2 ln [ 1 − e sin ϕ 1 + e sin ϕ ] = sinh − 1 ( tan ϕ ) − e tanh − 1 ( e sin ϕ ) = gd − 1 ( ϕ ) − e tanh − 1 ( e sin ϕ ) . {\displaystyle {\begin{aligned}\psi (\phi )&=\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\phi }{2}}\right)\right]+{\frac {e}{2}}\ln \left[{\frac {1-e\sin \phi }{1+e\sin \phi }}\right]\\&=\sinh ^{-1}(\tan \phi )-e\tanh ^{-1}(e\sin \phi )\\&=\operatorname {gd} ^{-1}(\phi )-e\tanh ^{-1}(e\sin \phi ).\end{aligned}}}
Para a projeção Normal Mercator (no elipsóide), essa função define o espaçamento dos paralelos: se o comprimento do equador na projeção for e (unidades de comprimento ou pixels), a distância, y, de um paralelo de latitude ϕ de o equador é
y ( ϕ ) = E 2 π ψ ( ϕ ) . {\displaystyle y(\phi )={\frac {E}{2\pi }}\psi (\phi )\,.}
A latitude isométrica ψ está intimamente relacionada à latitude conformada χ:
ψ ( ϕ ) = gd − 1 χ ( ϕ ) . {\displaystyle \psi (\phi )=\operatorname {gd} ^{-1}\chi (\phi )\,.}
Fórmulas e séries inversas
As fórmulas nas seções anteriores dão a latitude auxiliar em termos de latitude geodésica. As expressões para as latitudes geocêntricas e paramétricas podem ser invertidas diretamente, mas isso é impossível nos quatro casos restantes: as latitudes retificadoras, autônicas, conformes e isométricas. Existem dois métodos de processo.
The first is a numerical inversion of the defining equation for each and every particular value of the auxiliary latitude. The methods available are fixed-point iteration and Newton–Raphson root finding.When converting from isometric or conformal to geodetic, two iterations of Newton-Raphson gives double precision accuracy.The other, more useful, approach is to express the auxiliary latitude as a series in terms of the geodetic latitude and then invert the series by the method of Lagrange reversion. Such series are presented by Adams who uses Taylor series expansions and gives coefficients in terms of the eccentricity. Osborne derives series to arbitrary order by using the computer algebra package Maxima and expresses the coefficients in terms of both eccentricity and flattening. The series method is not applicable to the isometric latitude and one must find the conformal latitude in an intermediate step.Comparação numérica de latitudes auxiliares

O gráfico à direita mostra a diferença entre a latitude geodética e as latitudes auxiliares que não sejam a latitude isométrica (que diverge para o infinito nos pólos) para o caso do elipsóide WGS84. As diferenças mostradas no gráfico estão em minutos de arco. No hemisfério norte (latitudes positivas), θ ≤ χ ≤ μ ≤ ξ ≤ β ≤ ϕ; No hemisfério sul (latitudes negativas), as desigualdades são revertidas, com igualdade no equador e nos pólos. Embora o gráfico pareça simétrico em cerca de 45 °, o mínimo das curvas está realmente entre 45 ° 2 'e 45 ° 6'. Alguns pontos de dados representativos são fornecidos na tabela abaixo. As latitudes conformes e geocêntricas são quase indistinguíveis, um fato explorado nos dias das calculadoras manuais para acelerar a construção de projeções de mapa.
Para primeira ordem no achatamento de, as latitudes auxiliares podem ser expressas astante = ϕ - cf sin 2ϕ em onde a constante C assume os valores [1⁄2, 2⁄3, 3⁄4, 1, 1] para para = [β, ξ, μ, χ, θ].
Approximate difference from geodetic latitude (ϕ)ϕParametricβ − ϕAuthalicξ − ϕRectifyingμ − ϕConformalχ − ϕGeocentricθ − ϕ0°0.00′0.00′0.00′0.00′0.00′15°−2.88′−3.84′−4.32′−5.76′−5.76′30°−5.00′−6.66′−7.49′−9.98′−9.98′45°−5.77′−7.70′−8.66′−11.54′−11.55′60°−5.00′−6.67′−7.51′−10.01′−10.02′75°−2.89′−3.86′−4.34′−5.78′−5.79′90°0.00′0.00′0.00′0.00′0.00′Latitude e sistemas de coordenadas
A latitude geodética, ou qualquer uma das latitudes auxiliares definidas no elipsóide de referência, constitui com longitude um sistema de coordenadas bidimensionais nesse elipsóide. Para definir a posição de um ponto arbitrário, é necessário estender esse sistema de coordenadas em três dimensões. Três latitudes são usadas dessa maneira: as latitudes geodésicas, geocêntricas e paramétricas são usadas em coordenadas geodésicas, coordenadas polares esféricas e coordenadas elipsoidais, respectivamente.
Coordenadas geodésicas

Em um ponto arbitrário P, considere a linha PN que é normal ao elipsóide de referência. As coordenadas geodéticas p (ɸ, λ, h) são a latitude e a longitude do ponto n no elipsóide e na distância pn. Essa altura difere da altura acima da geóide ou de uma altura de referência, como a acima, o nível do mar médio em um local especificado. A direção do PN também diferirá da direção de uma linha de prumo vertical. A relação dessas diferentes alturas requer conhecimento da forma da geóide e também do campo de gravidade da terra.
Coordenadas polares esféricas

A latitude geocêntrica θ é o complemento do ângulo polar ou colatidão θ ′ nas coordenadas polares esféricas convencionais nas quais as coordenadas de um ponto são p (r, θ ′, λ), onde r é a distância de p do centro o, θ ′ É o ângulo entre o vetor de raio e o eixo polar e λ é longitude. Como o normal em um ponto geral no elipsóide não passa pelo centro, fica claro que os pontos P 'no normal, que todos têm a mesma latitude geodética, terão diferentes latitudes geocêntricas. Os sistemas de coordenadas polares esféricas são usadas na análise do campo da gravidade.
Coordenadas elipsoidais-harmônicas
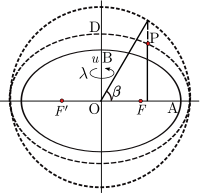
A latitude paramétrica também pode ser estendida a um sistema de coordenadas tridimensionais. Para um ponto P, não está no elipsóide de referência (semi-axos OA e OB), constrói um elipsóide auxiliar que é confocal (o mesmo foco f, f ′) com o elipsóide de referência: a condição necessária é que o produto Ae de eixo semi-major e a excentricidade é a mesma para os dois elipsóides. Seja você o eixo semi-minor (OD) do elipsóide auxiliar. Além disso, seja β a latitude paramétrica de P no elipsóide auxiliar. O conjunto (U, β, λ) define as coordenadas elipsoidais-harmônicas ou simplesmente coordenadas elipsoidais (embora esse termo também seja usado para se referir a coordenadas geodéticas). Essas coordenadas são a escolha natural nos modelos do campo de gravidade para um corpo elipsoidal rotativo. O acima se aplica a um elipsóide biaxial (um esferóide, como em coordenadas esferoidais oblatos); Para uma generalização, consulte coordenadas elipsoidais triaxiais.
Coordenar conversões
As relações entre os sistemas de coordenadas acima e também as coordenadas cartesianas não são apresentadas aqui. A transformação entre coordenadas geodésicas e cartesianas pode ser encontrada na conversão de coordenadas geográficas. A relação dos polares cartesianos e esféricos é dada no sistema de coordenadas esféricas. A relação das coordenadas cartesianas e elipsoidais é discutida em Torge.
Latitude astronômica
A latitude astronômica (φ) é o ângulo entre o plano equatorial e a direção vertical verdadeira em um ponto da superfície. A verdadeira vertical, a direção de uma linha de prumo, também é a direção da gravidade (o resultante da aceleração gravitacional (baseada em massa) e a aceleração centrífuga) nessa latitude. A latitude astronômica é calculada a partir de ângulos medidos entre o zênite e as estrelas cuja declinação é conhecida com precisão.
Em geral, a verdadeira vertical em um ponto da superfície não coincide exatamente com o elipsóide normal ao referência ou o normal ao geóide. O ângulo entre os normais astronômicos e geodéticos é chamado de deflexão vertical e geralmente é de alguns segundos de arco, mas é importante na geodesia. A razão pela qu






