Matemática e Arte

Content
Origens: da Grécia Antiga ao Renascença
O cânone e a simetria de Polykleitos

Polykleitos O ancião (c. 450-420 aC) era um escultor grego da Escola de Argos e contemporâneo de Phidias. Suas obras e estátuas consistiam principalmente de bronze e eram de atletas. De acordo com o filósofo e matemático Xenócrates, Polykleitos é classificado como um dos escultores mais importantes da antiguidade clássica por seu trabalho no Doryphorus e a estátua de Hera na heraion de Argos. Embora suas esculturas possam não ser tão famosas quanto as de Phidias, elas são muito admiradas. No seu cânone, um tratado que ele escreveu projetado para documentar as proporções corporais "perfeitas" do nu masculino, Polykleitos nos dá uma abordagem matemática para esculpir o corpo humano.
O cânone em si foi perdido, mas é conjecturado que os polikleitos usaram uma sequência de proporções em que cada comprimento é o da diagonal de um quadrado desenhado em seu antecessor, 1: √2 (cerca de 1: 1.4142).
A influência do cânone de Polykleitos é imensa na escultura clássica grega, romana e renascentista, muitos escultores seguindo a prescrição de Polykleitos. Enquanto nenhum dos trabalhos originais de Polykleitos sobrevive, cópias romanas demonstram seu ideal de perfeição física e precisão matemática. Alguns estudiosos argumentam que o pensamento pitagórico influenciou o cânone de Polykleitos. O cânone aplica os conceitos matemáticos básicos de geometria grega, como proporção, proporção e simetria (grego para "proporções harmoniosas") e a transforma em um sistema capaz de descrever a forma humana através de uma série de progressões geométricas contínuas.
Perspectiva e proporção

Nos tempos clássicos, em vez de tornar figuras distantes menores com perspectiva linear, objetos e figuras do tamanho de pintores de acordo com sua importância temática. Na Idade Média, alguns artistas usaram a perspectiva reversa para ênfase especial. O matemático muçulmano Alhazen (Ibn al-Haytham) descreveu uma teoria da óptica em seu livro de óptica em 1021, mas nunca a aplicou à arte. O Renascimento viu um renascimento da cultura e das idéias gregas e romanas clássicas, entre elas o estudo da matemática para entender a natureza e as artes. Dois principais motivos levaram artistas no final da Idade Média e o Renascimento em relação à matemática. Primeiro, os pintores precisavam descobrir como representar cenas tridimensionais em uma tela bidimensional. Segundo, filósofos e artistas estavam convencidos de que a matemática era a verdadeira essência do mundo físico e que todo o universo, incluindo as artes, poderia ser explicado em termos geométricos.
Os rudimentos da perspectiva chegaram com Giotto (1266/7 - 1337), que tentou atrair perspectiva usando um método algébrico para determinar a colocação de linhas distantes. Em 1415, o arquiteto italiano Filippo Brunelleschi e seu amigo Leon Battista Alberti demonstraram o método geométrico de aplicar a perspectiva em Florença, usando triângulos semelhantes aos formulados por Euclides, para encontrar a altura aparente de objetos distantes. As pinturas de perspectiva de Brunelleschi estão perdidas, mas a pintura da Santíssima Trindade de Masaccio mostra seus princípios no trabalho.

O piolo italiano Paolo Uccello (1397-1475) ficou fascinado pela perspectiva, como mostrado em suas pinturas da batalha de San Romano (c. 1435-1460): Lança quebrada está convenientemente ao longo das linhas de perspectiva.
O pintor Piero della Francesca (c. 1415-1492) exemplificou essa nova mudança no pensamento renascentista italiano. Ele era um especialista em matemático e geômetro, escrevendo livros sobre geometria e perspectiva sólida, incluindo De Prospectiva Pingendi (em perspectiva para pintura), Trattato d'Abaco (tratado de abacus) e De Quinque Corporibus regularibus (nos cinco sólidos regulares). O historiador Vasari, em suas vidas de pintores, chama Piero de "o maior geômetro de seu tempo, ou talvez de qualquer momento". O interesse de Piero em perspectiva pode ser visto em suas pinturas, incluindo o politicoso de Perugia, o retábulo de San Agostino e a flagelar de Cristo. Seu trabalho sobre geometria influenciou os matemáticos e artistas posteriores, incluindo Luca Pacioli em sua divina proporcione e Leonardo da Vinci. Piero estudou matemática clássica e as obras de Archimedes. Ele foi ensinado aritmético comercial em "Escolas Abacus"; Seus escritos são formatados como livros didáticos da Escola de Abacus, talvez incluindo o 1202 Liber Abaci de Leonardo Pisano (Fibonacci). A perspectiva linear estava apenas sendo introduzida no mundo artístico. Alberti explicou em seu 1435 de pictura: "Raios de luz viajam em linhas retas de pontos na cena observada para os olhos, formando uma espécie de pirâmide com o olho como vértice". Uma pintura construída com perspectiva linear é uma seção transversal dessa pirâmide.
Em De Prospectiva Pingendi, Piero transforma suas observações empíricas da maneira como os aspectos de uma figura mudam com o ponto de vista em provas matemáticas. Seu tratado começa na veia de Euclides: ele define o ponto como "a menor coisa que é possível para o olho compreender". Ele usa a lógica dedutiva para liderar o leitor à representação em perspectiva de um corpo tridimensional.
O artista David Hockney argumentou em seu livro Conhecimento secreto: redescobrindo as técnicas perdidas dos antigos mestres de que os artistas começaram a usar uma câmera Lucida a partir dos anos 1420, resultando em uma mudança repentina de precisão e realismo, e que essa prática foi continuada por grandes artistas, incluindo Ingres, Van Eyck e Caravaggio. Os críticos discordam se Hockney estava correto. Da mesma forma, o arquiteto Philip Steadman argumentou controversamente que Vermeer havia usado um dispositivo diferente, a câmera obscura, para ajudá -lo a criar suas pinturas distintamente observadas.
Em 1509, Luca Pacioli (c. 1447-1517) publicou de divina proporcione sobre proporção matemática e artística, inclusive no rosto humano. Leonardo da Vinci (1452-1519) ilustrou o texto com xilogravuras de sólidos regulares enquanto estudava com Pacioli nos anos 1490. Os desenhos de Leonardo são provavelmente as primeiras ilustrações de sólidos esqueletos. Estes, como os Rhombicuboctahedron, foram os primeiros a serem atraídos para demonstrar perspectiva, sendo sobrepostos um no outro. O trabalho discute a perspectiva dos trabalhos de Piero della Francesca, Melozzo da Forlì e Marco Palmezzano. Da Vinci estudou Summa de Pacioli, do qual ele copiava mesas de proporções. Em Mona Lisa e na Última Ceia, o trabalho de Da Vinci incorporou a perspectiva linear com um ponto de fuga para fornecer profundidade aparente. A última ceia é construída em uma proporção apertada de 12: 6: 4: 3, assim como a escola de Atenas de Raphael, que inclui Pitágoras com um tablet de proporções ideais, sagrado para os pitagóricos. No homem vitruviano, Leonardo expressou as idéias do arquiteto romano Vitruvius, mostrando inovador a figura masculina duas vezes e centralizando -o em um círculo e em um quadrado.
Já no século XV, a perspectiva curvilínea chegou às pinturas de artistas interessados em distorções de imagem. O retrato Arnolfini de Jan Van Eyck contém um espelho convexo com reflexões das pessoas na cena, enquanto o auto-retrato de Parmigianino em um espelho convexo, c. 1523–1524, mostra o rosto amplamente indistortado do artista no centro, com um fundo fortemente curvado e a mão do artista ao redor da borda.
O espaço tridimensional pode ser representado de forma convincente na arte, como no desenho técnico, por outros meios que não a perspectiva. As projeções oblíquas, incluindo a perspectiva do Cavalier (usadas por artistas militares franceses para representar fortificações no século XVIII), foram usados continuamente e onipresentes por artistas chineses desde o primeiro ou o segundo século até o século XVIII. Os chineses adquiriram a técnica da Índia, que a adquiriu da Roma antiga. A projeção oblíqua é vista na arte japonesa, como nas pinturas Ukiyo-e de Torii Kiyonaga (1752-1815).

Xilogravura do 1509 de divina de Luca Pacioli proporciona com um triângulo equilátero em um rosto humano

Câmera Lucida em uso. Scientific American, 1879

Ilustração de um artista usando uma câmera obscura. Século XVII

Proporção: o homem vitruviano de Leonardo, c. 1490

A teoria da perspectiva de Brunelleschi: trinità de Masaccio, c. 1426–1428, na Basílica de Santa Maria Novella
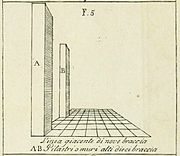
Diagrama de Leon Battista Alberti 1435 Della Pittura, com pilares em perspectiva em uma grade

Perspectiva linear na flagelação de Cristo de Piero della Francesca, c. 1455-1460

Perspectiva curvilínea: espelho convexo no retrato Arnolfini de Jan Van Eyck, 1434

Parmigianino, auto-retrato em um espelho convexo, c. 1523–1524

Pitágoras com tablet de proporções, na Escola de Atenas de Rafael, 1509

Projeção oblíqua: entrada e quintal de um iço. Detalhes de Scroll sobre Suzhou por Xu Yang, ordenado pelo imperador Qianlong. século 18

Projeção oblíqua: Mulheres jogando Shogi, Go e Ban-Sugoroku Board Games. Pintura de Torii Kiyonaga, Japão, c. 1780
proporção áurea
A proporção dourada (aproximadamente igual a 1,618) era conhecida por Euclides. A proporção dourada foi reivindicada persistentemente nos tempos modernos para ter sido usada em arte e arquitetura pelos antigos no Egito, Grécia e em outros lugares, sem evidências confiáveis. A reivindicação pode derivar de confusão com "média dourada", que para os gregos antigos significava "evitar o excesso em qualquer direção", não uma proporção. Piramidologistas desde o século XIX argumentaram por motivos matemáticos duvidosos para a proporção dourada no design da pirâmide. O Parthenon, um templo de BC do século V em Atenas, foi reivindicado usar a proporção de ouro em sua fachada e planta, mas essas reivindicações também são refutadas pela medição. A Grande Mesquita de Kairouan, na Tunísia, também se afirma usar a proporção de ouro em seu design, mas a proporção não aparece nas partes originais da mesquita. O historiador da arquitetura Frederik Macody Lund argumentou, em 1919 fazer o caso dele. Outros estudiosos argumentam que até o trabalho de Pacioli em 1509, a proporção dourada era desconhecida de artistas e arquitetos. Por exemplo, a altura e a largura da frente de Notre-Dame de Laon têm a proporção 8/5 ou 1,6, não 1.618. Tais taxas de Fibonacci rapidamente se tornam difíceis de distinguir da proporção dourada. Após Pacioli, a proporção dourada é mais definitivamente discernível nas obras de arte, incluindo Mona Lisa, de Leonardo.
Outra proporção, o único outro número mórfico, foi nomeado número de plástico em 1928 pelo arquiteto holandês Hans van Laan (originalmente chamado Le Nombre Radiant em francês). Seu valor é a solução da equação cúbica
x 3 = x + 1 {\displaystyle x^{3}=x+1\,} ,
,um número irracional que é aproximadamente 1,325. Segundo o arquiteto Richard Padovan, isso possui índices característicos 3/4 e 1/7, que governam os limites da percepção humana em relacionar um tamanho físico a outro. Van der Laan usou essas proporções ao projetar a Igreja da Abadia de St. Benedictusberg de 1967 na Holanda.
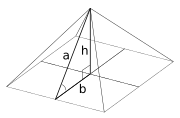
Base: as taxas de hipotenusa (B: A) para a pirâmide de Khufu podem ser: 1: φ (triângulo Kepler), 3: 5 (3-4-5 Triângulo) ou 1: 4/π

Razões supostas: Notre-Dame de Laon

Retângulos de ouro sobrepostos na Mona Lisa

A Igreja da Abadia de St. Benedictusberg de 1967 de Hans van der Laan tem proporções de número de plástico.
Simetrias planas

Simetrias planas foram exploradas por milênios em obras de arte, como tapetes, treliças, têxteis e inclinações.
Muitos tapetes tradicionais, sejam tapetes de estacas ou kilims de malha plana, são divididos em um campo central e uma borda de enquadramento; Ambos podem ter simetrias, embora em tapetes tecidos à mão sejam frequentemente um pouco quebrados por pequenos detalhes, variações de padrão e mudanças na cor introduzida pelo tecelão. Em Kilims da Anatólia, os motivos usados são geralmente simétricos. O layout geral também está geralmente presente, com arranjos como listras, listras alternando com fileiras de motivos e matrizes embaladas de motivos aproximadamente hexagonais. O campo é comumente preparado como um papel de parede com um grupo de papel de parede como o PMM, enquanto a borda pode ser apresentada como um friso do grupo friso PM11, PMM2 ou PMA2. Os kilims turcos e da Ásia Central geralmente têm três ou mais fronteiras em diferentes grupos de frisos. Os tecelões certamente tinham a intenção de simetria, sem conhecimento explícito de sua matemática. O matemático e teórico da arquitetura Nikos Salingaros sugere que a "presença poderosa" (efeito estético) de um "grande tapete", como os melhores tapetes de dois medalhões do século XVII, é criado por técnicas matemáticas relacionadas às teorias do arquiteto Christófeiro Alexander. Essas técnicas incluem tornar o oposto casal; valores de cores opostos; áreas diferenciando geometricamente, seja usando formas complementares ou equilibrando a direcionalidade de ângulos nítidos; fornecendo complexidade em pequena escala (do nível do nó para cima) e da simetria pequena e em larga escala; Repetindo elementos em uma hierarquia de diferentes escalas (com uma proporção de cerca de 2,7 de cada nível para o próximo). Salingaros argumenta que "todos os tapetes de sucesso satisfazem pelo menos nove das dez regras acima" e sugere que pode ser possível criar uma métrica a partir dessas regras.
Latices elaborados são encontrados no trabalho de jali indiano, esculpido em mármore para adornar túmulos e palácios. Lattices chineses, sempre com alguma simetria, existem em 14 dos 17 grupos de papel de parede; Eles geralmente têm espelho, espelho duplo ou simetria rotacional. Alguns têm um medalhão central e outros têm uma fronteira em um grupo de frisos. Muitas redes chinesas foram analisadas matematicamente por Daniel S. Dye; Ele identifica Sichuan como o centro do ofício.
As simetrias são proeminentes em artes têxteis, incluindo acolchoado, tricô, ponto cruz, crochê, bordado e tecelagem, onde podem ser puramente decorativos ou podem ser marcas de status. A simetria rotacional é encontrada em estruturas circulares, como cúpulas; Às vezes, estes são elaboradamente decorados com padrões simétricos por dentro e por fora, como na mesquita Sheikh Lotfollah de 1619 em Isfahan. Itens de bordados e trabalhos de renda, como toalhas de mesa e tapetes de mesa, fabricados usando bobinas ou tatting, podem ter uma grande variedade de simetrias refletidas e rotacionais que estão sendo exploradas matematicamente.
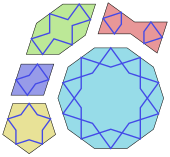
A arte islâmica explora simetrias em muitas de suas formas de arte, principalmente em Girih Tilings. Estes são formados usando um conjunto de cinco formas de ladrilhos, a saber, um decágono regular, um hexágono alongado, uma gravata borboleta, um rombus e um pentágono comum. Todos os lados desses ladrilhos têm o mesmo comprimento; E todos os seus ângulos são múltiplos de 36 ° (π/5 radianos), oferecendo simetrias de cinco e dez vezes. Os ladrilhos são decorados com linhas de cinta (girih), geralmente mais visíveis que os limites de ladrilhos. Em 2007, os físicos Peter Lu e Paul Steinhardt argumentaram que Girih se assemelhava a Tilings Quasicrystaline Penrose. A elaborada Tilework Geométrica Zellige é um elemento distinto na arquitetura marroquina. Os cofres muqarnas são tridimensionais, mas foram projetados em duas dimensões com desenhos de células geométricas.

Hotamis Kilim (detalhe), Central Anatolia, início do século 19

Detalhes de um brocado da dinastia Ming, usando um padrão de rede hexagonal chanfrado

Madeira de mármore Jaali em Tomb de Salim Chishti, Fatehpur Sikri, Índia

Symmetries: Trabalho de tapeçaria de padrões de bargello florentino

Teto da mesquita do sheikh lotfollah, Isfahan, 1619

Simetria rotacional em renda: trabalho de tatting

Tilhas de girih: padrões em grandes e pequenas escalas em um spandrel do santuário Darb-i imam, Isfahan, 1453

Tessellations: Zellige Mosaic Tiles em Bou Inania Madrasa, FES, Marrocos

A complexa geometria e inclinações da muqarnas abrem na mesquita Sheikh Lotfollah, Isfahan

Plano do arquiteto de um cofre de Muqarnas. Topkapı Scroll

TUPA Inca Tunic do Peru, 1450 –1540, um têxtil andino que denota alta classificação
Polyedra

Os sólidos platônicos e outros poliedros são um tema recorrente na arte ocidental. Eles são encontrados, por exemplo, em um mosaico de mármore com o pequeno dodecaedro estrelado, atribuído a Paolo Uccello, no chão da Basílica de San Marco em Veneza; Nos diagramas de Leonardo da Vinci de poliedros regulares desenhados como ilustrações para o livro 1509 de Luca Pacioli, a proporção divina; como um rhombicuboctahedron de vidro no retrato de Pacioli de Jacopo de Barbari, pintado em 1495; no poliedro truncado (e em vários outros objetos matemáticos) na melencolia da gravura de Albrecht Dürer; e na pintura de Salvador Dalí, a última ceia na qual Cristo e seus discípulos são retratados dentro de um dodecaedro gigante.
Albrecht Dürer (1471-1528) foi um gravador renascentista alemão que fez contribuições importantes para a literatura poliédrica em seu livro de 1525, Underweysung der Messung (educação sobre medição), destinada a ensinar os assuntos da perspectiva linear, geometria na arquitetura, sólidos platônicos e e e sólidos e e sólidos e sólidos e sólidos e medições), destinados a ensinar os assuntos da perspectiva linear, geometria na arquitetura, sólidos platônicos e e Polígonos regulares. Dürer provavelmente foi influenciado pelas obras de Luca Pacioli e Piero Della Francesca durante suas viagens à Itália. Embora os exemplos de perspectiva em Underweysung der Messung sejam subdesenvolvidos e contêm imprecisões, há uma discussão detalhada sobre poliedros. Dürer também é o primeiro a introduzir em texto a idéia de redes poliédricas, o poliedro se desenrolou para ficar plano para impressão. Dürer publicou outro livro influente sobre proporções humanas, chamado Vier Bücher von Menschlicher, proporção (quatro livros sobre proporção humana) em 1528.
A bem conhecida Melencolia de Gravura de Dürer, descrevo um pensador frustrado sentado por um trapezohedron triangular truncado e uma praça mágica. Esses dois objetos, e a gravura como um todo, foram objeto de uma interpretação mais moderna do que o conteúdo de quase qualquer outra impressão, incluindo um livro de dois volumes de Peter-Klaus Schuster, e uma discussão influente na monografia de Dürer de Erwin Panofsky de Dürer .
A pintura de Salvador Dalí em 1954, corpus hypercubus, descreve exclusivamente a cruz de Cristo como uma rede tridimensional desdobrada para um hipercubo, também conhecido como tesserato: o desdobramento de um teserato nesses oito cubos é análogo a desdobrar os lados de um cubo em um cruzamento forma de seis quadrados, aqui representando a perspectiva divina com um poliedro regular quadridimensional. A pintura mostra a figura de Cristo em frente ao tesarato; Ele normalmente seria mostrado fixado com unhas na cruz, mas não há unhas na pintura. Em vez disso, existem quatro pequenos cubos em frente ao corpo, nos cantos da frente dos oito cubos de tesarato. O matemático Thomas Banchoff afirma que Dalí estava tentando ir além do mundo tridimensional, enquanto o poeta e a crítica de arte Kelly Grovier diz que "a pintura parece ter rachado o vínculo entre a espiritualidade da salvação de Cristo e a materialidade da geométrica e física Forças. Parece preencher a divisão que muitos sentem separação da ciência da religião ".

A primeira ilustração impressa de um Rhombicuboctahedron, de Leonardo da Vinci, publicado em De Divina Proporcione, 1509

Icosaedro como parte do monumento a Baruch Spinoza, Amsterdã
Dimensões fractais

Os desenhos tradicionais do resistência a cera indonésios em tecidos combinam motivos representacionais (como elementos florais e vegetais) com elementos abstratos e um tanto caóticos, incluindo a imprecisão na aplicação da resistência de cera e variação aleatória introduzida pela rachadura da cera. Os desenhos da Batik têm uma dimensão fractal entre 1 e 2, variando em diferentes estilos regionais. Por exemplo, o batik de Cirebon tem uma dimensão fractal de 1,1; Os Batiks de Yogyakarta e Surakarta (Solo) em Java Central têm uma dimensão fractal de 1,2 a 1,5; e os Batiks de Lasem, na costa norte de Java e de Tasikmalaya, em Java Ocidental, têm uma dimensão fractal entre 1,5 e 1,7.
As obras de pintura de gotejamento do artista moderno Jackson Pollock são igualmente distintas em sua dimensão fractal. Seu número 14 de 1948 tem uma dimensão semelhante à costa de 1,45, enquanto suas pinturas posteriores tinham dimensões fractais sucessivamente mais altas e, portanto, padrões mais elaborados. Um de seus últimos trabalhos, Blue Pols, levou seis meses para criar e tem a dimensão fractal de 1,72.
Um relacionamento complexo
O astrônomo Galileo Galilei em seu Il Saggiatore escreveu que "[o universo] está escrito na linguagem da matemática, e seus personagens são triângulos, círculos e outras figuras geométricas". Os artistas que se esforçam e procuram estudar a natureza devem primeiro, na visão de Galileu, entender completamente a matemática. Os matemáticos, por outro lado, procuraram interpretar e analisar a arte através das lentes da geometria e da racionalidade. O matemático Felipe Cucker sugere que a matemática, e especialmente a geometria, é uma fonte de regras para a "criação artística orientada por regras", embora não seja a única. Algumas das muitas vertentes do relacionamento complexo resultante são descritas abaixo.

Matemática como uma arte
O matemático Jerry P. King descreve a matemática como uma arte, afirmando que "as chaves da matemática são beleza e elegância e não embotamento e técnico", e que a beleza é a força motivadora para a pesquisa matemática. King cita o ensaio matemático de G. H. Hardy em 1940, o pedido de matemática. Nele, Hardy discute por que ele encontra dois teoremas dos tempos clássicos como primeira taxa, a prova de Euclides de que existem infinitamente muitos números primos e a prova de que a raiz quadrada de 2 é irracional. King avalia esse último contra os critérios de Hardy para a elegância matemática: "Senhora, profundidade, generalidade, inesperada, inevitabilidade e economia" (itálico de King) e descreve a prova como "esteticamente agradável". O matemático húngaro Paul Erdős concordou que a matemática possuía beleza, mas considerou as razões além da explicação: "Por que os números são bonitos? É como perguntar por que é a nona sinfonia de Beethoven. Os números são lindos. "
Ferramentas matemáticas para arte
A matemática pode ser discernida em muitas das artes, como música, dança, pintura, arquitetura e escultura. Cada um deles está ricamente associado à matemática. Entre as conexões com as artes visuais, a matemática pode fornecer ferramentas para artistas, como as regras da perspectiva linear, conforme descrito por Brook Taylor e Johann Lambert, ou os métodos de geometria descritiva, agora aplicados na modelagem de software de sólidos, datando para Albrecht Dürer e Gaspard Monge. Artistas de Luca Pacioli na Idade Média e Leonardo da Vinci e Albrecht Dürer no Renascimento fizeram uso e desenvolveram idéias matemáticas na busca de seu trabalho artístico. O uso da perspectiva começou, apesar de alguns usos embrionários na arquitetura da Grécia antiga, com pintores italianos como Giotto no século XIII; Regras como o ponto de fuga foram formuladas pela primeira vez por Brunelleschi em cerca de 1413, sua teoria influenciando Leonardo e Dürer. O trabalho de Isaac Newton no espectro óptico influenciou a teoria das cores de Goethe e, por sua vez, artistas como Philipp Otto Runge, J. M. W. Turner, os pré-rafaelitas e Wassily Kandinsky. Os artistas também podem optar por analisar a simetria de uma cena. As ferramentas podem ser aplicadas por matemáticos que estão explorando arte, ou artistas inspirados em matemática, como M. C. Escher (inspirado em H. S. M. Coxeter) e o arquiteto Frank Gehry, que mais tenuosamente argumentou que o design auxiliado por computador lhe permitiu se expressar em um novo novo caminho.

O artista Richard Wright argumenta que objetos matemáticos que podem ser construídos podem ser vistos "como processos para simular fenômenos" ou como obras de "arte do computador". Ele considera a natureza do pensamento matemático, observando que os fractais eram conhecidos pelos matemáticos por um século antes de serem reconhecidos como tal. Wright conclui afirmando que é apropriado sujeitar objetos matemáticos a quaisquer métodos usados para "chegar a um acordo com artefatos culturais como arte, tensão entre objetividade e subjetividade, seus significados metafóricos e caráter dos sistemas representacionais". Ele fornece como instâncias uma imagem do conjunto Mandelbrot, uma imagem gerada por um algoritmo de autômato celular e uma imagem renderizada por computador, e discute, com referência ao teste de Turing, se produtos algorítmicos podem ser arte. Sasho Kalajdzievski Matemática e Arte: Uma Introdução à Matemática Visual adota uma abordagem semelhante, observando tópicos de matemática visual adequadamente visual, como inclinações, fractais e geometria hiperbólica.
Algumas das primeiras obras de arte do computador foram criadas pela "Drawing Machine 1" de Desmond Paul Henry, uma máquina analógica baseada em um computador bombizante e exibida em 1962. A máquina era capaz de criar uma linha complexa, abstrata, assimétrica, curvilínea, mas repetitiva desenhos. Mais recentemente, Hamid Naderi Yeganeh criou formas sugestivas de objetos do mundo real, como peixes e pássaros, usando fórmulas que são sucessivamente variadas para atrair famílias de curvas ou linhas angulares. Artistas como Mikael Hvidtfeldt Christensen criam obras de arte generativa ou algorítmica escrevendo scripts para um sistema de software como o Synth Synth: o artista direciona efetivamente o sistema para aplicar uma combinação desejada de operações matemáticas a um conjunto de dados escolhido.

Escultura matemática por Bathsheba Grossman, 2007

Escultura fractal: 3d Fraktal 03/h/dd por Hartmut Skerbisch, 2003

Palavra de Fibonacci: Detalhe da obra de arte de Samuel Monnier, 2009

Imagem de arte do computador produzida por "Drawing Machine 1" de Desmond Paul Henry, exibida em 1962

Um pássaro em voo, de Hamid Naderi Yeganeh, 2016, construído com uma família de curvas matemáticas.
Da matemática à arte

O matemático e o físico teórico Henri Poincaré Ciência e Hipótese foi amplamente lido pelos cubistas, incluindo Pablo Picasso e Jean Metzinger. Estando muito familiarizado com o trabalho de Bernhard Riemann sobre geometria não euclidiana, Poincaré estava mais do que ciente de que a geometria euclidiana é apenas uma das muitas configurações geométricas possíveis, e não como uma verdade objetiva absoluta. A possível existência de uma quarta dimensão inspirou artistas a questionar a perspectiva clássica do Renascença: a geometria não euclidiana se tornou uma alternativa válida. O conceito de que a pintura poderia ser expressa matematicamente, em cores e forma, contribuiu para o cubismo, o movimento artístico que levou à arte abstrata. Metzinger, em 1910, escreveu que: "[Picasso] estabelece uma perspectiva móvel gratuita, da qual esse engenhoso matemático Maurice Princet deduziu uma geometria inteira". Mais tarde, Metzinger escreveu em suas memórias:
Maurice Princet se juntou a nós com frequência ... era como artista que ele conceituava a matemática, como esteticista que ele invocou continuos n-dimensionais. Ele adorava atrair os artistas nas novas visões sobre o espaço que foram abertas por Schlegel e alguns outros. Ele conseguiu nisso.
O impulso de tornar modelos de ensino ou pesquisa de formas matemáticas naturalmente cria objetos que têm simetrias e formas surpreendentes ou agradáveis. Alguns deles inspiraram artistas como o homem de dadaístas Ray, Marcel Duchamp e Max Ernst, e seguindo Man Ray, Hiroshi Sugimoto.

Man Ray fotografou alguns dos modelos matemáticos do instituto Henri Poincaré em Paris, incluindo a matemática de Objet (objeto matemático). Ele observou que isso representava superfícies enneper com curvatura negativa constante, derivada da pseudo-esfera. Essa base matemática era importante para ele, pois lhe permitia negar que o objeto era "abstrato", alegando que era tão real quanto o mictório que Duchamp transformou em uma obra de arte. Man Ray admitiu que a fórmula [enneper de superfície] do objeto "não significava nada para mim, mas as próprias formas eram tão variadas e autênticas quanto qualquer outra natureza". Ele usou suas fotografias dos modelos matemáticos como figuras em sua série que ele fez nas peças de Shakespeare, como sua pintura de 1934 pintando Antony e Cleópatra. O repórter de arte Jonathan Keats, escrevendo na vida Forbeslife, argumenta que Man Ray fotografou "os parabolóides elípticos e pontos cônicos na mesma luz sensual que suas imagens de Kiki de Montparnasse", e "repelina engenhosamente os cálculos legais de matemática para revelar a topologia da topologia da desejo". Escultores do século XX, como Henry Moore, Barbara Hepworth e Naum Gabo, se inspiraram nos modelos matemáticos. Moore escreveu sobre sua mãe e filho com cordas de 1938: "Sem dúvida, a fonte de minhas figuras de cordas era o Museu da Ciência ... Fiquei fascinado pelos modelos matemáticos que vi lá ... não foi o estudo científico desses modelos, mas os Capacidade de examinar as cordas como com uma gaiola de pássaros e ver uma forma dentro de outra que me excitou. "

Os artistas Theo Van Dodburg e Piet Mondrian fundaram o movimento De Stijl, que eles queriam "estabelecer um vocabulário visual composto por formas geométricas elementares compreensíveis por todos e adaptáveis a qualquer disciplina". Muitas de suas obras de arte consistem visivelmente de quadrados e triângulos governados, às vezes também com círculos. Os artistas de Stijl trabalharam em pintura, móveis, design de interiores e arquitetura. Após o rompimento de De Stijl, Van Do Donsburg fundou o movimento de concreto artístico de vanguarda, descrevendo sua composição aritmética de 1929-1930, uma série de quatro quadrados pretos na diagonal de um fundo quadrado, como "uma estrutura que pode ser controlada, a A. superfície definitiva sem elementos ou capricho individual ", mas" sem falta de espírito, não falta o universal e não ... vazio, pois há tudo o que se encaixa no ritmo interno ". O crítico de arte Gladys Fabre observa que duas progressões estão em ação na pintura, a saber, os crescentes quadrados pretos e os fundos alternados.
A matemática de tesellation, poliedros, modelagem do espaço e auto-referência, desde que o artista gráfico M. C. Escher (1898-1972) com a vida de materiais para suas xilogravuras. No esboço de Alhambra, Escher mostrou que a arte pode ser criada com polígonos ou formas regulares, como triângulos, quadrados e hexágonos. Escher usou polígonos irregulares ao amarrar o plano e frequentemente usou reflexões, reflexões de deslizamento e traduções para obter outros padrões. Muitos de seus trabalhos contêm construções impossíveis, feitas usando objetos geométricos que estabelecem uma contradição entre projeção de perspectiva e três dimensões, mas são agradáveis para a visão humana. Ascendente e descendente de Escher são baseadas na "escada impossível" criada pelo cientista médico Lionel Penrose e seu filho, o matemático Roger Penrose.
Alguns dos muitos desenhos de tesellation de Escher foram inspirados em conversas com o matemático H. S. M. Coxeter sobre geometria hiperbólica. Escher estava especialmente interessado em cinco poliedros específicos, que aparecem muitas vezes em seu trabalho. Os sólidos platônicos - tetraedrons, cubos, octaedros, dodecaedros e icosaedros - são especialmente proeminentes em ordem e caos e quatro sólidos regulares. Essas figuras estreladas geralmente residem em outra figura, o que distorce ainda mais o ângulo de visualização e a conformação dos poli -hedrons e fornece uma obra de arte de perspectiva multifacetada.
A complexidade visual de estruturas matemáticas, como teselações e poliedros, inspirou uma variedade de obras de arte matemáticas. Stewart Coffin faz quebra -cabeças poliédricos em bosques raros e bonitos; George W. Hart trabalha sobre a teoria dos objetos de poliedros e esculturas inspirados por eles; Magnus Wenninger faz modelos "especialmente bonitos" de poliedros estrelados complexos.
As perspectivas distorcidas da anamorfose foram exploradas na arte desde o século XVI, quando Hans Holbein, o jovem, incorporou um crânio severamente distorcido em seus 1533 pintando os embaixadores. Muitos artistas desde então, incluindo Escher, fazem uso de truques anamórficos.
A matemática da topologia inspirou vários artistas nos tempos modernos. O escultor John Robinson (1935–2007) criou obras como Gordian Knot e bandas de amizade, exibindo a teoria dos nós no bronze polido. Outros trabalhos de Robinson exploram a topologia das torusas. A Gênesis é baseada em anéis Borromean - um conjunto de três círculos, dois dos quais link, mas em que toda a estrutura não pode ser desmontada sem quebrar. O escultor Helaman Ferguson cria superfícies complexas e outros objetos topológicos. Seus trabalhos são representações visuais de objetos matemáticos; O óctuplo Way é baseado no grupo Linear PSL (2,7) projetivo, um grupo finito de 168 elementos. A Bathsheba Grossman escultor baseia -se da mesma forma seu trabalho em estruturas matemáticas. O artista Nelson Saiers incorpora conceitos e teoremas matemáticos em sua arte, desde toposes e esquemas até o teorema das quatro cores e a irracionalidade de π.
Um projeto de investigação de artes liberais examina as conexões entre matemática e arte através da faixa de Möbius, Flexgons, Origami e Panorama Photography.
Objetos matemáticos, incluindo o coletor Lorenz e o plano hiperbólico, foram criados usando artes de fibra, incluindo crochê. O tecelão americano Ada Dietz escreveu uma expressões algébricas monografistas de 1949 em tecidos tecidos à mão, definindo padrões de tecelagem com base na expansão dos polinômios multivariados. O matemático Daina Taimiņa demonstrou características do plano hiperbólico por crochê em 2001. Isso levou Margaret e Christine Wertheim a crochê um recife de coral, consistindo em muitos animais marinhos, como nudibrâncias cujas formas são baseadas em planos hiperbólicos. O matemático J. C. P. Miller usou o autômato celular da Regra 90 para projetar tapeçarias representando árvores e padrões abstratos de triângulos. Os "Mathekniticians" Pat Ashforth e Steve Plummer usam versões de malha de objetos matemáticos, como os hexaflexágonos em seus ensinamentos, embora sua esponja de homens se mostrasse muito problemática para tricotar e fosse feita de tela plástica. Seu projeto "Mathghans" (afegãs para escolas) introduziu o tricô no currículo britânico de matemática e tecnologia.
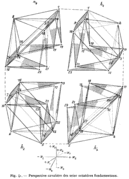
Espaço quadridimensional para o cubismo: traité de ESPrit Jouffret de 1903, dimensões de Géomérie à Quatre.

De Stijl: Theo van faz composição geométrica de Burg I (Still Life), 1916

Pedagogia à arte: Magnus Wenninger com alguns de seus poliedros estrelados, 2009

Um lenço de tira de Möbius em Crochet, 2007

Anamorfismo: os embaixadores de Hans Holbein the Younger, 1533, com crânio severamente distorcido em primeiro plano

Recife de coral crochê: muitos animais modelados como planos hiperbólicos com parâmetros variados de Margaret e Christine Wertheim. Föhr Reef, Tübingen, 2013

Ilustrando matemática


A modelagem está longe de ser a única maneira possível de ilustrar conceitos matemáticos. O triptico Stefaneschi de Giotto, 1320, ilustra a recursão na forma de Mise en Abyme; O painel central do tríptico contém, inferior esquerdo, a figura ajoelhada do cardeal Stefaneschi, segurando o tríptico como uma oferta. As pinturas metafísicas de Giorgio de Chirico, como seu grande interior metafísico de 1917, exploram a questão dos níveis de representação na arte, representando pinturas em suas pinturas.
A arte pode exemplificar paradoxos lógicos, como em algumas pinturas do surrealista René Magritte, que pode ser lido como piadas semióticas sobre confusão entre os níveis. Na condição de LA Humaine (1933), Magritte descreve um cavalete (na tela real), apoiando perfeitamente uma vista através de uma janela que é enquadrada por cortinas "reais" na pintura. Da mesma forma, a Escher's Print Gallery (1956) é uma impressão que mostra uma cidade distorcida que contém uma galeria que contém recursivamente a imagem e, portanto, ad infinitum. Magritte fez uso de esferas e cubóides para distorcer a realidade de uma maneira diferente, pintando-os ao lado de uma variedade de casas em sua aritmética mental de 1931 como se fossem blocos de construção de crianças, mas em tamanho doméstico. O Guardian observou que a "imagem de Toytown Sierie" profetizou a usurpação do modernismo de "formas tradicionais aconchegantes", mas também brinca com a tendência humana de buscar padrões na natureza.

A última pintura de Salvador Dalí, The Swallow's Tail (1983), fazia parte de uma série inspirada na teoria da catástrofe de René Thom. O pintor e escultor espanhol Pablo Palazuelo (1916–2007) focou na investigação do formulário. Ele desenvolveu um estilo que descreveu como a geometria da vida e a geometria de toda a natureza. Consistindo em formas geométricas simples com padronização e coloração detalhadas, em obras como Angular I e Automnes, Palazuelo se expressou em transformações geométricas.
O artista Adrian Gray pratica o equilíbrio de pedra, explorando o atrito e o centro de gravidade para criar composições impressionantes e aparentemente impossíveis.

Os artistas, no entanto, não necessariamente tomam geometria literalmente. Como Douglas Hofstadter escreve em sua reflexão de 1980 sobre o pensamento humano, Gödel, Escher, Bach, por meio de (entre outras coisas) da matemática da arte: "A diferença entre um desenho de escher e geometria não-euclidiana é que, no último, compreensível As interpretações podem ser encontradas para os termos indefinidos, resultando em um sistema total compreensível, enquanto que para o primeiro, o resultado final não é reconciliável com a concepção do mundo, não importa quanto tempo se olha para as fotos ". Hofstadter discute a galeria de impressão de litografia aparentemente paradoxal de M. C. Escher; Ele descreve uma cidade litorânea contendo uma galeria de arte que parece conter uma pintura da cidade litorânea, existe um "laço estranho ou hierarquia emaranhada" aos níveis de realidade na imagem. O próprio artista, observa Hofstadter, não é visto; Sua realidade e sua relação com a litografia não são paradoxais. O vazio central da imagem também atraiu o interesse dos matemáticos Bart de Smit e Hendrik Lenstra, que propõem que ele possa conter uma cópia do efeito de Droste, girada e encolhida; Esta seria uma ilustração adicional de recursão além da observada por Hofstadter.
Análise da história da arte
A análise algorítmica de imagens de obras de arte, por exemplo, usando a espectroscopia de fluorescência de raios-X, pode revelar informações sobre arte. Tais técnicas podem descobrir imagens em camadas de tinta posteriormente cobertas por um artista; Ajude os historiadores da arte a visualizar uma obra de arte antes que ela rache ou desbotasse; Ajude a contar uma cópia de um original ou distinguir o estilo de pincelada de um mestre dos de seus aprendizes.

O estilo de pintura de gotejamento de Jackson Pollock tem uma dimensão fractal definitiva; Entre os artistas que podem ter influenciado o caos controlado de Pollock, Max Ernst pintou figuras de Lissajous diretamente balançando um balde de tinta perfurado sobre uma tela.
O cientista da computação Neil Dodgson investigou se as pinturas de listras de Bridget Riley poderiam ser caracterizadas matematicamente, concluindo que, embora a distância da separação pudesse "fornecer alguma caracterização" e a entropia global trabalhou em algumas pinturas, a autocorrelação falhou quando os padrões de Riley eram irregulares. A entropia local funcionou melhor e se correlacionou bem com a descrição dada pelo crítico de arte Robert Kudielka.
A medida estética do matemático americano George Birkhoff em 1933 propõe uma métrica quantitativa da qualidade estética de uma obra de arte. Ele não tenta medir as conotações de uma obra, como o que uma pintura pode significar, mas é limitada aos "elementos da ordem" de uma figura poligonal. Birkhoff combina primeiro (como uma soma) cinco desses elementos: se existe um eixo vertical de simetria; se há equilíbrio óptico; Quantas simetrias rotacionais ele possui; Como é a figura do papel de parede; e se existem recursos insatisfatórios, como ter dois vértices muito próximos. Essa métrica, O, leva um valor entre -3 e 7. A segunda métrica, C, conta elementos da figura, que para um polígono é o número de linhas retas diferentes contendo pelo menos um de seus lados. Birkhoff define então sua medida estética da beleza de um objeto como o/c. Isso pode ser interpretado como um equilíbrio entre o prazer de olhar para o objeto dá e a quantidade de esforço necessária para aceitar. A proposta de Birkhoff foi criticada de várias maneiras, principalmente por tentar colocar a beleza em uma fórmula, mas ele nunca alegou ter feito isso.
Estímulos à pesquisa matemática
A arte às vezes estimula o desenvolvimento da matemática, como quando a teoria da perspectiva de Brunelleschi em arquitetura e pintura iniciou um ciclo de pesquisa que levou ao trabalho de Brook Taylor e Johann Heinrich Lambert sobre os fundamentos matemáticos do desenho de perspectiva e, finalmente, à matemática de matemática de Geometria Projectiva de Girard Desargues e Jean-Vittor PoncElet.
A arte japonesa de dobra de papel de origami foi reformulada matematicamente por Tomoko Fusé usando módulos, pedaços de papel congruentes, como quadrados e transformá-los em poliedros ou inclinações. A dobra de papel foi usada em 1893 por T. Sundara Rao em seus exercícios geométricos em dobramento de papel para demonstrar provas geométricas. A matemática do dobramento de papel foi explorada no teorema de Maekawa, no teorema de Kawasaki e nos axiomas de Huzita -Hatori.

Estímulo à geometria projetiva: o diagrama de Alberti mostrando um círculo visto em perspectiva como uma elipse. Della Pittura, 1435-1436

Origami Matemático: Spring em ação, de Jeff Beynon, feita de um único retângulo de papel.
Ilusão para Op Art

Ilusões ópticas como a Fraser Spiral demonstram surpreendentemente limitações na percepção visual humana, criando o que o historiador da arte Ernst Gombrich chamou de "truque desconcertante". As cordas pretas e brancas que parecem formar espirais são de fato círculos concêntricos. O meados do século XX OP art ou o estilo de arte óptica de pintura e gráficos explorou esses efeitos para criar a impressão de movimento e padrões piscantes ou vibratórios vistos no trabalho de artistas como Bridget Riley, Spyros Horemis e Victor Vasarely.
Geometria sagrada
Uma fita de arte da Grécia antiga vê Deus como o geômetro do mundo, e a geometria do mundo, portanto, como sagrada. A crença de que Deus criou o universo de acordo com um plano geométrico tem origens antigas. Plutarco atribuiu a crença a Platão, escrevendo que "Platão disse que Deus geometra continuamente" (Convivialium Disputuationum, Liber 8,2). Esta imagem influenciou o pensamento ocidental desde então. O conceito platônico derivou por sua vez de uma noção pitagórica de harmonia na música, onde as notas foram espaçadas em proporções perfeitas, correspondendo aos comprimentos das cordas da lira; De fato, os pitagóricos sustentaram que tudo era organizado por número. Da mesma forma, no pensamento platônico, os sólidos regulares ou platônicos ditam as proporções encontradas na natureza e no art. Uma iluminação no Codex Vindobonensis do século XIII mostra a Deus desenhando o universo com um par de bússolas, que podem se referir a um versículo no Antigo Testamento: "Quando ele estabeleceu os céus, eu estava lá: quando ele colocou uma bússola no rosto do profundo "(Provérbios 8:27) ,. Em 1596, o astrônomo matemático Johannes Kepler modelou o universo como um conjunto de sólidos platônicos aninhados, determinando os tamanhos relativos das órbitas dos planetas. O antigo dos dias de William Blake (representando Urizen, a personificação de Blake de razão e lei) e sua pintura do físico Isaac Newton, nu, curvado e desenhando com uma bússola, use o simbolismo das bússolas para criticar a razão convencional e o materialismo como tacanho. A crucificação de Salvador Dalí de 1954 (Corpus Hypercubus) descreve a cruz como um hipercubo, representando a perspectiva divina com quatro dimensões, em vez dos três usuais. No Sacramento de The Last Ceia de Dalí (1955), Cristo e seus discípulos são retratados dentro de um dodecaedro gigante.

Deus, o geômetro. Codex Vindobonensis, c. 1220

A criação, com o rolamento de pantocrator. Bíblia de St Louis, c. 1220–1240

O modelo platônico de espaçamento planetário de Johannes Kepler no sistema solar de Mysterium cosmográfico, 1596

William Blake, The Ancient of Days, 1794

William Blake's Newton, c. 1800






