N-vetor
Content
Propriedades gerais
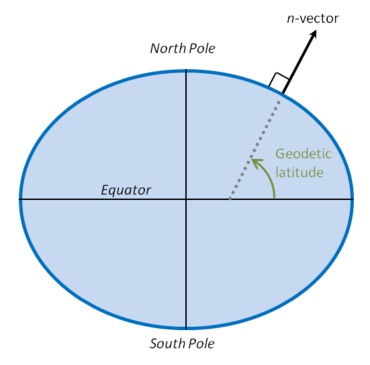
Um vetor normal para uma superfície estritamente convexa pode ser usada para definir exclusivamente uma posição de superfície. N-vetor é um vetor normal de apontamento externo, com comprimento da unidade usado como representação de posição.
Para a maioria das aplicações, a superfície é o elipsóide de referência da Terra e, portanto, o vetor N é usado para representar uma posição horizontal. Portanto, o ângulo entre o vetor n e o plano equatorial corresponde à latitude geodética, como mostrado na figura.

Uma posição de superfície tem dois graus de liberdade e, portanto, dois parâmetros são suficientes para representar qualquer posição na superfície. No elipsóide de referência, a latitude e a longitude são parâmetros comuns para esse fim, mas, como todas as representações de dois parâmetros, elas têm singularidades. Isso é semelhante à orientação, que possui três graus de liberdade, mas todas as representações de três parâmetros têm singularidades. Nos dois casos, as singularidades são evitadas adicionando um parâmetro extra, ou seja, para usar o vetor n (três parâmetros) para representar a posição horizontal e um quaternion da unidade (quatro parâmetros) para representar a orientação.
O vetor n é uma representação individual, o que significa que qualquer posição de superfície corresponde a um vetor N exclusivo e qualquer vetor N corresponde a uma posição de superfície única.
Como um vetor 3D euclidiano, a álgebra vetorial 3D padrão pode ser usada para os cálculos de posição, e isso faz com que o N-vetor seja adequado para a maioria dos cálculos de posição horizontal.
Conversão de latitude/longitude em N-vetor
Com base na definição do sistema de coordenadas ECEF, chamado E, fica claro que passar da latitude/longitude para N-vetor, é alcançado por:
n e = [ cos ( l a t i t u d e ) cos ( l o n g i t u d e ) cos ( l a t i t u d e ) sin ( l o n g i t u d e ) sin ( l a t i t u d e ) ] {\displaystyle \mathbf {n} ^{e}=\left[{\begin{matrix}\cos(\mathrm {latitude} )\cos(\mathrm {longitude} )\\\cos(\mathrm {latitude} )\sin(\mathrm {longitude} )\\\sin(\mathrm {latitude} )\\\end{matrix}}\right]}
O Superscript E significa que o vetor n é decomposto no sistema de coordenadas e (isto é, o primeiro componente é a projeção escalar do vetor n no eixo x de e, o segundo no eixo y de E etc.). Observe que a equação é exata para o modelo de terra esférica e elipsoidal.
Converter n-vetor em latitude/longitude
Dos três componentes do vetor n, n x e {\ displaystyle n_ {x}^{e}}, n y e {\ displaystyle n_ {y}^{e}} e n z e {\ displaystyle n_ {z}^{e} }, a latitude pode ser encontrada usando:
l a t i t u d e = arcsin ( n z e ) = arctan ( n z e n x e 2 + n y e 2 ) {\displaystyle \mathrm {latitude} =\arcsin \left(n_{z}^{e}\right)=\arctan \left({\frac {n_{z}^{e}}{\sqrt {{n_{x}^{e}}^{2}+{n_{y}^{e}}^{2}}}}\right)}
A expressão mais à direita é mais adequada para a implementação do programa de computador.
A longitude é encontrada usando:
l o n g i t u d e = arctan ( n y e n x e ) {\displaystyle \mathrm {longitude} =\arctan \left({\frac {n_{y}^{e}}{n_{x}^{e}}}\right)}
Nessas expressões, o arctan (y / x) {\ displayStyle \ arctan (y / x)} deve ser implementado usando uma chamada para atan2 (y, x). A singularidade do polo da longitude é evidente, pois o atan2 (0,0) é indefinido. Observe que as equações são exatas para o modelo de terra esférica e elipsoidal.
Exemplo: Grande Distância do Círculo
Encontrar a grande distância do círculo entre duas posições horizontais (assumindo a terra esférica) é geralmente feita por meio de latitude e longitude. Três expressões diferentes para essa distância são comuns; O primeiro é baseado no ArcCOS, o segundo é baseado no Arcsin e a final é baseada no Arctan. As expressões, que são sucessivamente mais complexas para evitar instabilidades numéricas, não são fáceis de encontrar e, como são baseadas em latitude e longitude, as singularidades do pólo podem se tornar um problema. Eles também contêm deltas de latitude e longitude, que em geral devem ser usados com cuidado próximo ao meridiano de ± 180 ° e aos pólos.
A solução do mesmo problema usando o vetor N é mais simples devido à possibilidade de usar álgebra vetorial. A expressão de Arccos é alcançada a partir do produto DOT, enquanto a magnitude do produto cruzado fornece a expressão da arcsina. Combinar os dois dá a expressão do Arctan:
Δ σ = arccos ( n a ⋅ n b ) Δ σ = arcsin ( | n a × n b | ) Δ σ = arctan ( | n a × n b | n a ⋅ n b ) {\displaystyle {\begin{aligned}&\Delta \sigma =\arccos \left(\mathbf {n} _{a}\cdot \mathbf {n} _{b}\right)\\&\Delta \sigma =\arcsin \left(\left|\mathbf {n} _{a}\times \mathbf {n} _{b}\right|\right)\\&\Delta \sigma =\arctan \left({\frac {\left|\mathbf {n} _{a}\times \mathbf {n} _{b}\right|}{\mathbf {n} _{a}\cdot \mathbf {n} _{b}}}\right)\\\end{aligned}}}
onde n a {\ displayStyle \ mathbf {n} _ {a}} e n b {\ displayStyle \ mathbf {n} _ {b}} são os vetores n que representam as duas posições A e B. Δ σ {\ displayStyle \ delta \ sigma} é a diferença angular e, portanto, a distância de grande círculo é alcançada multiplicando-se com o raio da terra. Essa expressão também funciona nos pólos e no meridiano de ± 180 °.
Existem vários outros exemplos em que o uso da álgebra vetorial simplifica os problemas padrão. Para uma comparação geral das várias representações, consulte a página de representações de posição horizontal.






