Ondas topográficas de Rossby

Derivação física

Esta seção descreve a situação matematicamente mais simples, onde as ondas topográficas Rossby se formam: uma inclinação de fundo uniforme.

Equações de águas rasas

Um sistema de coordenadas é definido com X na direção leste, y na direção norte e z como a distância da superfície da Terra. As coordenadas são medidas a partir de uma certa coordenada de referência na superfície da Terra com uma latitude de referência φ 0 {\ displaystyle \ varphi _ {0}} e uma espessura média da camada de referência H 0 {\ displayStyle H_ {0}}. A derivação começa com as equações de águas rasas:

∂ u ∂ t + u ∂ u ∂ x + v ∂ u ∂ y - f 0 v = - g ∂ η ∂ x ∂ v ∂ t + u ∂ v ∂ x + v ∂ v ∂ y + f 0 u = - g g ∂ η ∂ y ∂ η ∂ t + ∂ ∂ x h u + ∂ ∂ y h v = 0, {\ displaystyle {\ Begin {alinhado} {\ parcial u \ over \ parcial t} & + u {\ parcial u \ over \ parcial x X }+v {\ parcial u \ over \ parcial y} -f_ {0} v = -g {\ parcial \ eta \ over \ parcial x} \\ [3pt] {\ parcial v \ over \ parcial t} &+ u {\ parcial v \ over \ parcial x}+v {\ parcial v \ over \ parcial y}+f_ {0} u = -g {\ parcial \ eta \ over \ parcial y} \\ [3pt] {\ Parcial \ eta \ over \ parcial t} &+{\ parcial \ over \ parcial x} hu+{\ parcial \ over \ parcial y} hv = 0, \ end {alinhado}}}

Onde

u {\displaystyle u} is the velocity in the x direction, or zonal velocity v {\displaystyle v} is the velocity in the y direction, or meridional velocity h ' is the local and instantaneous fluid layer thickness η {\displaystyle \eta } is the height deviation of the fluid from its mean height g {\displaystyle g} is the acceleration due to gravity f 0 {\displaystyle f_{0}} is the Coriolis parameter at the reference coordinate with f 0 = 2 Ω sin ⁡ ( φ 0 ) {\displaystyle f_{0}=2\Omega \sin(\varphi _{0})} , where Ω {\displaystyle \Omega } is the angular frequency of the Earth and φ 0 {\displaystyle \varphi _{0}} is the reference latitude

Na equação acima, o atrito (arrasto viscoso e viscosidade cinemática) é negligenciado. Além disso, é assumido um parâmetro de Coriolis constante ("aproximação do plano F"). A primeira e a segunda equação das equações de águas rasas são chamadas de equações de momento zonal e meridional, e a terceira equação é a equação de continuidade. As equações de águas rasas assumem um fluido homogêneo e barotrópico.

Linearização

Por simplicidade, o sistema é limitado por meio de uma inclinação inferior fraca e uniforme que está alinhada com o eixo y, que por sua vez permite uma melhor comparação com os resultados com as ondas planetárias de Rossby. A espessura média da camada h {\ displayStyle h} para um fluido não perturbado é então definido como

H = h 0 + α 0 y com α = | α 0 | L H 0 ≪ 1, {\ displayStyle h = h_ {0}+\ alpha _ {0} y \ qquad {\ text {com}} \ \ qquad \ alpha = {\ esquerda \ vert \ alpha _ {0} \ \ \ \ Vert l \ over h_ {0}} \ ll 1,}

onde α 0 {\ displayStyle \ alpha _ {0}} é a inclinação do fundo, α {\ displayStyle \ alpha} o parâmetro topográfico e l {\ displayStyle l} a escala de comprimento horizontal do movimento. A restrição no parâmetro topográfico garante que exista uma irregularidade fraca no fundo. A espessura local e instantânea do líquido H 'pode ser escrita como

h (x, y, t) = h 0 + α 0 y + η (x, y, t). {\ displayStyle h (x, y, t) = h_ {0}+\ alpha _ {0} y+\ eta (x, y, t).}

Utilizando essa expressão na equação de continuidade das equações rasas de águas

∂ η ∂ t + (u ∂ η ∂ x + v ∂ η ∂ y) + η (∂ u ∂ x + ∂ v ∂ y) + (h 0 + α 0 y) (∂ u ∂ x + ∂ v ∂ y y y )+α 0 v = 0. {\ displayStyle {\ parcial \ eta \ over \ parcial t}+\ esquerda (u {\ parcial \ eta \ over \ parcial x}+v {\ parcial \ eta \ over \ parcial y } \ direita)+\ eta \ esquerda ({\ parcial u \ over \ parcial x}+{\ parcial v \ over \ parcial y} \ right)+(h_ {0}+\ alfa _ {0} y) \ Esquerda ({\ parcial u \ over \ parcial x}+{\ parcial v \ over \ parcial y} \ direita)+\ alpha _ {0} v = 0.}

O conjunto de equações é feito linear para obter um conjunto de equações que é mais fácil de resolver analiticamente. Isso é feito assumindo um número Rossby RO (= advecção / força coriolis), que é muito menor que o número de rossby temporal Rot (= força de inércia / coriolis). Além disso, a escala de comprimento de η {\ displaystyle \ eta} Δ h {\ displayStyle \ delta h} é assumida como muito menor que a espessura do fluido h {\ displaystyle h}. Finalmente, a condição no parâmetro topográfica é usada e o seguinte conjunto de equações lineares é obtido:

∂ u ∂ t - f 0 v = - g ∂ η ∂ x ∂ v ∂ t + f 0 u = - g ∂ η ∂ y ∂ η ∂ t + h 0 (∂ u ∂ x + ∂ v ∂ y) + α 0 v = 0. {\ displayStyle {\ Begin {alinhado} {\ parcial u \ over \ parcial t} &-f_ {0} v = -g {\ parcial \ eta \ over \ parcial x} \\ [3pt] {\ parcial v \ over \ parcial t} &+f_ {0} u = -g {\ parcial \ eta \ over \ parcial y} \\ [3pt] {\ parcial \ eta \ over \ parcial t} &+h_ {0} \ esquerda ({\ parcial u \ over \ parcial x}+{\ parcial v \ over \ parcial y} \ right)+\ alpha _ {0} v = 0. \ End {alinhado}}}}}

Aproximação quase-geoestófica

Em seguida, a aproximação quase-geoestófica

u = u ¯ + u ~ com u ¯ = - g f 0 ∂ η ∂ y v = v ¯ + v ~ com v ¯ = g f u}}+{\ tilde {u}} \ qquad & {\ text {com}} \ qquad {\ bar {u}} =-{g \ over f_ {0}} {\ parcial \ eta \ over \ parcial y} \\ [3pt] v = {\ bar {v}}+{\ tilde {v}} \ qquad & {\ text {com}} \ qquad {\ bar {v}} = {g \ over f_ {{ 0}} {\ parcial \ eta \ over \ parcial x}, \\ [3pt] \ end {alinhado}}}

onde u ¯ {\ displayStyle {\ bar {u}}} e v ¯ {\ displayStyle {\ bar {v}}} são os componentes de fluxo geoestrófico e u ~ {\ displaystyle {\ tilde {u}}} e v ~ {\ displayStyle {\ tilde {v}}} são os componentes do fluxo da idade com u ~ ¯ ¯ {\ displayStyle {\ tilde {u}} \ ll {\ bar {u}}} e v ~ ≪ v {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ displaystyle {\ tilde {v}} \ ll {\ bar {v}}}. Substituindo essas expressões por u {\ displaystyle u} e v {\ displaystyle v} no conjunto de equações adquiridas anteriormente, rendimentos:

- g f H 0 (∂ u ~ ∂ x + ∂ v ~ ∂ y) + α 0 g f }} {\ parcial ^{2} \ eta \ over \ parcial y \ parcial t}+{\ parcial {\ tilde {u}} \ over \ parcial t} -f_ {0} {\ tilde {v} = = = 0 \\ [3pt] & {g \ over f_ {0}} {\ parcial ^{2} \ eta \ over \ parcial x \ parcial t}+{\ parcial {\ tilde {v}} \ over \ parcial t }+f_ {0} {\ tilde {u}} = 0 \\ [3pt] & {\ parcial \ eta \ over \ parcial t}+h_ {0} \ esquerda ({\ parcial {\ tilde {u}}}} \ over \ parcial x}+{\ parcial {\ tilde {v}} \ over \ parcial y} \ right)+\ alpha _ {0} {g \ over f_ {0}} {\ parcial \ eta \ over \ Parcial x}+\ alpha _ {0} {\ tilde {v}} = 0. \ end {alinhado}}}

Negligenciando os termos em que os pequenos termos de componentes (u ~, v ~, ∂ t {\ displaystyle {\ tilde {u}}, {\ tilde {v}}, {\ parcial \ over \ parcial t}} e α 0 {\ DisplayStyle \ alpha _ {0}}) são multiplicados, as expressões obtidas são:

v ~ = - g f 0 2 ∂ 2 η ∂ y ∂ t u ~ = - g f 0 2 ∂ 2 η ∂ x ∂ t ∂ η ∂ t + h 0 (∂ u ~ ∂ x + ∂ v ~ ∂ y) + α 0 g f 0 ∂ η ∂ x = 0. {\ displayStyle {\ Begin {alinhado} & {\ tilde {v}} =-{g \ over f_ {0} ^{2}} {\ parcial ^{2} \ eta \ over \ parcial y \ parcial t} \\ [3pt] & {\ tilde {u}} =-{g \ over f_ {0} ^{2}} {\ parcial ^{2} \ eta \ over \ parcial x \ parcial t} \\ [3pt] & {\ parcial \ eta \ over \ parcial t}+h_ {0} \ esquerda ({\ parcial {\ tilde {u}} \ over \ parcial x}+{\ parcial {\ tilde {v}} \ over \ parcial y} \ right)+\ alpha _ {0} {g \ over f_ {0}} {\ parcial \ eta \ over \ parcial x} = 0. \ end {alinhado }}}

Substituindo os componentes da velocidade da idade da idade na equação de continuidade, é obtido o seguinte resultado:

∂ η ∂ t-r 2 ∂ ∂ t ∇ 2 η + α 0 g f \ parcial t} \ nabla ^{2} \ eta +\ alpha _ {0} {g \ over f_ {0}} {\ parcial \ eta \ over \ parcial x} = 0,}

em que r, o raio de Rossby de deformação, é definido como

R = g h 0 f 0. {\ displayStyle r = {{\ sqrt {gh_ {0}}} \ over f_ {0}}.}

Relação de dispersão

Levando para η {\ displaystyle \ eta} uma onda monocromática plana da forma

η = a cos ⁡ (k x x + k y y-ω t + ϕ), {\ displayStyle \ eta = a \ cos (k_ {x} x + k_ {y} y- \ omega t + \ phi),}

com um {\ displayStyle a} a amplitude, k x {\ displaystyle k_ {x}} e k y {\ displaystyle k_ {y}} o número de onda na direção x e y, respectivamente, ω {\ displaystyle \ omega} a frequência angular da onda e ϕ {\ displayStyle \ phi} um fator de fase, é obtida a seguinte relação de dispersão para ondas topográficas de Rossby:

ω = α 0 g f 0 k x 1 + r 2 (k x 2 + k y 2). {\ displayStyle \ omega = {\ alpha _ {0} g \ over f_ {0}} {k_ {x} \ over 1+r^{2} (k_ {x}^{2}+k_ {y}^ {2})}.}

Se não houver inclinação inferior (α 0 = 0 {\ displayStyle \ alpha _ {0} = 0}), a expressão acima não gera ondas, mas um fluxo constante e geoestófico. Esta é a razão pela qual essas ondas são chamadas de ondas topográficas de Rossby.

A frequência máxima das ondas topográficas de Rossby é

| ω | m a x = | α 0 | G 2 | f 0 | R, {\ displayStyle \ esquerda \ vert \ omega \ direita \ vert _ {max} = {\ esquerd Vert r},}

que é alcançado para k x = r-1 {\ displayStyle k_ {x} = r^{-1}} e k y = 0 {\ displayStyle k_ {y} = 0}. Se o forçamento criar ondas com frequências acima desse limite, nenhuma onda de Rossby será gerada. Esta situação raramente acontece, a menos que α 0 {\ displaystyle \ alpha _ {0}} seja muito pequeno. Em todos os outros casos | ω | m a x {\ displayStyle \ esquerd \ vert \ omega \ direita \ vert _ {max}} excede | f 0 | {\ displayStyle \ esquerda \ vert f_ {0} \ direita \ vert} e a teoria quebra. A razão para isso é que as condições assumidas: α ≪ 1 {\ DisplayStyle \ alpha \ ll 1} e Rot ≪ 1 {\ DisplayStyle \ ll 1} não são mais válidas. As equações de águas rasas usadas como ponto de partida também permitem outros tipos de ondas, como ondas de Kelvin e ondas de gravidade de inércia (ondas de Poincaré). No entanto, estes não aparecem nos resultados obtidos devido à suposição quase-geoestófica, que é usada para obter esse resultado. Na dinâmica de ondas, isso é chamado de filtragem.

Velocidade de fase

A velocidade de fase das ondas ao longo dos isobatas (linhas de igual profundidade, aqui a direção x) é

c x = ω k x = α 0 g f 0 1 1 + r 2 (k x 2 + k y 2), {\ displaystyle c_ {x} = {\ omega \ over k_ {x}} = {\ alpha _ {0} g \ sobre f_ {0}} {1 \ sobre 1+r^{2} (k_ {x}^{2}+k_ {y}^{2})},}

o que significa que no hemisfério norte as ondas se propagam com o lado raso à direita e no hemisfério sul com o lado raso à sua esquerda. A equação de c x {\ displayStyle c_ {x}} mostra que a velocidade de fase varia com o número de onda para que as ondas sejam dispersivas. O máximo de C X {\ DisplayStyle C_ {x}} é

| c x | m a x = α 0 g f 0, {\ displayStyle \ left \ vert c_ {x} \ right \ vert _ {max} = {\ alpha _ {0} g \ over f_ {0},},}

que é a velocidade de ondas muito longas (k x 2 + k y 2 → 0 {\ displaystyle k_ {x}^{2} + k_ {y}^{2} \ rightarrow 0}). A velocidade de fase na direção y é

c y = ω k y = k x k y c x, {\ displaystyle c_ {y} = {\ omega \ over k_ {y}} = {k_ {x} \ sobre k_ {y}} c_ {x},}

o que significa que C y {\ displayStyle C_ {y}} pode ter algum sinal. A velocidade de fase é dada por

c = ω k = k x k c x, {\ displayStyle c = {\ omega \ over k} = {k_ {x} \ sobre k} c_ {x},}

Do qual pode ser visto que | c | ≤ | c x | ware k | = k x 2 + k y 2 ≥ | k x | ware }. Isso implica que o máximo de | c x | {\ displayStyle \ esquerd \ vert c_ {x} \ right \ vert} é o máximo de | c | {\ displayStyle \ esquerda \ vert C \ Right \ Vert}.

Analogia entre ondas topográficas e planetárias Rossby

As ondas Rossby planetárias e topográficas são as mesmas no sentido de que, se o termo α 0 g / f 0 {\ displaystyle {\ alpha _ {0} g / f_ {0}}} é trocado por - β 0 r 2 {\ DisplayStyle -\ beta _ {0} r^{2}} nas expressões acima, onde β 0 {\ displaystyle \ beta _ {0}} é o parâmetro beta -paramétrico ou rossby, a expressão de ondas planetárias é obtida. A razão para essa semelhança é que, para as equações de águas rasas não lineares para um fluxo homogêneo e sem atrito, a vorticidade potencial q é conservada:

d q d t = 0 com q = ζ + f h, {\ displayStyle {dq \ over dt} = 0 \ qquad {\ text {com}} \ qquad q = {\ zeta + f \ over h},}

com ζ {\ displaystyle \ zeta} sendo a vorticidade relativa, que é o dobro da velocidade de rotação dos elementos fluidos sobre o eixo z e é matematicamente definido como

ζ = ∂ v ∂ x − ∂ u ∂ y, {\ displayStyle \ zeta = {\ parcial v \ over \ parcial x}-{\ parcial u \ over \ parcial y},}

com ζ> 0 {\ displayStyle \ zeta> 0} Uma rotação anti-horário em torno do eixo z. Em um plano beta e para um fundo linearmente inclinado na direção meridional, a vorticidade potencial se torna

q = f 0 + β 0 y + ζ h 0 + α 0 y + η. {\ displayStyle q = {f_ {0}+\ beta _ {0} y+\ zeta \ over h_ {0}+\ alpha _ {0} y+\ eta}.}.

Nas derivações acima, foi assumido que

β 0 L ≪ | f 0 | : número planetário pequeno β [ζ] ≪ | f 0 | : pequeno número rossby ro α 0 l ≪ h 0: pequeno parâmetro topográfico α Δ h ≪ h: dinâmica linear, {\ displayStyle {\ begin {alinhed} \ beta _ {0} l \ ll \ left \ vert f_ {0} \ right \ vert & {\ text {: pequeno número planetário}} \ beta \\ [3pt] [\ zeta] \ ll \ left \ vert f_ {0} \ direita \ vert & {\ text {: small rossby número ro }} \\ [3pt] \ alpha _ {0} l \ ll h_ {0} & {\ text {: pequeno parâmetro topográfico}} \ alpha \\ [3pt] \ delta h \ ll h & {\ text {: linear Dynamics}}, \ end {alinhado}}}

assim

q = f 0 (1 + β 0 y f 0 + ζ f 0) h 0 (1 + α 0 y h 0 + η h 0) = f 0 h 0 (1 + β 0 y f 0 + ζ f 0) (1 − Α 0 y H 0 - η h 0+…), {\ displayStyle q = {f_ {0} \ esquerda (1+{\ beta _ {0} y \ over f_ {0}}+{\ zeta \ over f_ {0}} \ direita) \ over h_ {0} \ esquerda (1+{\ alpha _ {0} y \ over h_ {0}}+{\ eta \ over h_ {0}} \ direita)} = {f_ {0} \ over h_ {0}} \ esquerda (1+{\ beta _ {0} y \ over f_ {0}}+{\ zeta \ over f_ {0}} \ direita) \ esquerda (1 -{\ alpha _ {0} y \ over h_ {0}}-{\ eta \ over h_ {0}}+\ ldots \ right),}

onde uma expansão de Taylor foi usada no denominador e os pontos indicam termos de ordem superior. Somente mantendo os maiores termos e negligenciando o resto, é obtido o seguinte resultado:

q ≈ f 0 h 0 (1 + β 0 y f 0 + ζ f 0 - α 0 y h 0 - η h 0). {\ displayStyle q \ aprox {f_ {0} \ over h_ {0}} \ esquerd {\ alpha _ {0} y \ over h_ {0}}-{\ eta \ over h_ {0}} \ right).}

Consequentemente, a analogia que aparece em potencial vorticidade é que β 0 / f 0 {\ displaystyle \ beta _ {0} / f_ {0}} e -α 0 / h 0 {\ displaystyle -\ alpha _ {0} / h_ {0}} desempenham o mesmo papel na equação de vorticidade potencial. Reescrevendo estes termos de maneira um pouco diferente, isso se resume ao visto anterior -β 0 r 2 {\ displayStyle -\ beta _ {0} r^{2}} e α 0 g / f 0 {\ displaystyle {\ alpha _ { 0} g/f_ {0}}}, que demonstra a semelhança entre ondas planetárias e topográficas de Rossby. A equação para a vorticidade potencial mostra que as ondas planetárias e topográficas de Rossby existem por causa de um gradiente de fundo em potencial vorticidade.

A analogia entre ondas planetárias e topográficas de Rossby é explorada em experimentos de laboratório que estudam fluxos geofísicos para incluir o efeito beta, que é a mudança do parâmetro coriolis sobre a Terra. Os vasos de água usados ​​nesses experimentos são pequenos demais para que o parâmetro coriolis varie significativamente. O efeito beta pode ser imitado até certo ponto nesses experimentos usando um tanque com um fundo inclinado. A substituição do efeito beta por um fundo inclinada é válida apenas para uma inclinação suave, movimentos lentos do fluido e na ausência de estratificação.

Explicação conceitual

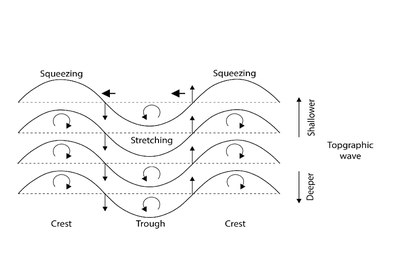
Como mostrado na última seção, as ondas Rossby são formadas porque a vorticidade potencial deve ser conservada. Quando a superfície tem uma inclinação, a espessura da camada de fluido H 'não é constante. A conservação da vorticidade potencial força a vorticidade relativa ζ {\ displayStyle \ zeta} ou o parâmetro coriolis f {\ displaystyle f} para mudar. Como o parâmetro coriolis é constante em uma determinada latitude, a vorticidade relativa deve mudar. Na figura, um fluido se move para um ambiente mais raso, onde H 'é menor, fazendo com que o fluido forme uma crista. Quando a altura é menor, a vorticidade relativa também deve ser menor. Na figura, isso se torna uma vorticidade relativa negativa (no hemisfério norte, uma rotação no sentido horário) mostrada com as setas arredondadas. No hemisfério sul, isso é uma rotação no sentido anti -horário, porque o parâmetro coriolis é negativo no hemisfério sul. Se um fluido se move para um ambiente mais profundo, o oposto é verdadeiro. A parcela fluida na profundidade original é imprensada entre duas parcelas fluidas, com uma delas com uma vorticidade relativa positiva e a outra uma vorticidade relativa negativa. Isso causa um movimento da parcela fluida à esquerda na figura. Em geral, o deslocamento causa um padrão de onda que se propaga com o lado mais raso à direita no hemisfério norte e à esquerda no hemisfério sul.

Medições de ondas topográficas de Rossby na Terra

De 1 de janeiro de 1965 a 1 de janeiro de 1968, o projeto BOOY na instituição oceanográfica de Woods Hole lançou bóias no lado oeste do Atlântico norte para medir as velocidades. Os dados têm várias lacunas porque algumas das bóias desapareceram. Ainda assim, eles conseguiram medir ondas topográficas de Rossby a 500 metros de profundidade. Vários outros projetos de pesquisa confirmaram que existem de fato ondas topográficas de Rossby no Atlântico do Norte.

Em 1988, as ondas barotrópicas planetárias Rossby foram encontradas na bacia do noroeste do Pacífico. Pesquisas adicionais realizadas em 2017 concluíram que as ondas Rossby não são ondas planetárias de Rossby, mas ondas topográficas de Rossby.

Em 2021, a pesquisa no Mar da China Meridional confirmou que existem ondas topográficas de Rossby.