Projeção gnomônica
Content
História
Diz -se que a projeção gnomônica é a projeção de mapa mais antiga, desenvolvida por Thales para mapas de estrelas no século VI aC. O caminho da ponta das sombras ou do ponto de luz em um relógio de sol baseado em Nodus traça as mesmas hiperbolas formadas por paralelos em um mapa gnomônico.
Propriedades
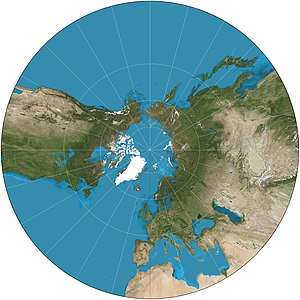
A projeção gnomônica é do centro de uma esfera para uma tangente plana à esfera (Fig 1 abaixo). A esfera e o avião tocam no ponto tangente. Grandes círculos se transformam em linhas retas através da projeção gnomônica. Como os meridianos (linhas de longitude) e o equador são grandes círculos, eles sempre são mostrados como linhas retas em um mapa gnomônico. Como a projeção é do centro da esfera, um mapa gnomônico pode representar menos da metade da área da esfera. A distorção da escala do mapa aumenta do centro (ponto tangente) para a periferia.
If the tangent point is one of the poles then the meridians are radial and equally spaced (Fig 2 below). The equator cannot be shown as it is at infinity in all directions. Other parallels (lines of latitude) are depicted as concentric circles.If the tangent point is on the equator then the meridians are parallel but not equally spaced (Fig 3 below). The equator is a straight line perpendicular to the meridians. Other parallels are depicted as hyperbolae.If the tangent point is not on a pole or the equator, then the meridians are radially outward straight lines from a pole, but not equally spaced (Fig 4 below). The equator is a straight line that is perpendicular to only one meridian, indicating that the projection is not conformal. Other parallels are depicted as conic sections.
Fig 1. Um grande círculo se projeta para uma linha reta na projeção gnomônica
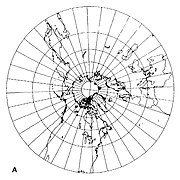
Fig 2. projeção gnomônica centrada no pólo norte
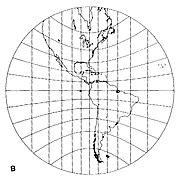
Fig 3. projeção gnomônica centrada no equador
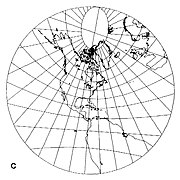
Fig 4. projeção gnomônica centrada em latitude 40 graus norte
Como em todas as projeções azimutais, os ângulos do ponto tangente são preservados. A distância do mapa desse ponto é uma função r (d) da verdadeira distância d, dada por
r ( d ) = R tan d R {\displaystyle r(d)=R\,\tan {\frac {d}{R}}}
onde r é o raio da terra. A escala radial é
r ′ ( d ) = 1 cos 2 d R {\displaystyle r'(d)={\frac {1}{\cos ^{2}{\frac {d}{R}}}}}
e a escala transversal
1 cos d R {\displaystyle {\frac {1}{\cos {\frac {d}{R}}}}}
Portanto, a escala transversal aumenta externamente e a escala radial ainda mais.
Usar
As projeções gnomônicas são usadas no trabalho sísmico porque as ondas sísmicas tendem a viajar por grandes círculos. Eles também são usados pelas marinhas na plotagem de rolamentos de direção, já que os sinais de rádio viajam por grandes círculos. Os meteoros também viajam por grandes círculos, com o Atlas Gnomonic Brno 2000.0 sendo o conjunto recomendado por gráficos estrelas da IMO para observações visuais de meteoros. Os pilotos de aeronaves e navios usam a projeção para encontrar a rota mais curta entre o início e o destino.
A projeção gnomônica é usada extensivamente na fotografia, onde é chamada de projeção retilínea. Por serem equivalentes, o mesmo espectador usado para panoramas fotográficos pode ser usado para renderizar mapas gnomônicos (veja como um panorama interativo de 360 °).
A projeção gnomônica é usada na astronomia, onde o ponto tangente está centrado no objeto de interesse. A esfera projetada neste caso é a esfera celestial, r = 1, e não a superfície da terra.







