Regra de Naismith

Content

Suposições e cálculos

Ritmo em minutos por quilômetro ou milha vs. ângulo de inclinação resultante da regra do Naísmo para velocidades basais de 5 e 4 km / h.

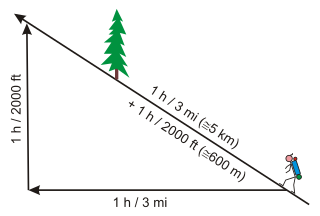
A regra do Naismith original de 1892 diz que se deve permitir uma hora por cinco quilômetros no mapa e uma hora adicional por 2000 pés de subida. Está incluído na última frase de seu relatório de uma viagem.

Hoje é formulado de várias maneiras. 1 h / 3 mi + 1 h / 2000 ft de Naismith pode ser substituído por:

1 h / 3 mi (5 km) + 1 h / 2000 ft (600 m)1 h / 5 km (3 mi) + 1/2 h / 300 m (1000 ft)3 mph + ½ h / 1000 ft5 km/h + ½ h / 300 m12 min / 1 km + 10 min / 100 m

A regra básica assume caminhantes de aptidão razoável, em terrenos típicos e em condições normais. Ele não explica atrasos, como pausas prolongadas para descanso ou passeios turísticos ou por obstáculos de navegação. Para o planejamento das expedições, um líder da equipe pode usar a regra da NAISMITH para montar um cartão de rota. [Citação necessária]

É possível aplicar ajustes ou "correções" para um terreno mais desafiador, embora não possa ser usado para embarcar em rotas. No sistema de classificação usado na América do Norte, a regra de Naismith se aplica apenas a caminhadas classificadas pela Classe 1 no sistema decimal de Yosemite, e não à classe 2 ou superior. [Citação necessária]

Na prática, os resultados da regra do Naísmo são geralmente considerados o tempo mínimo necessário para concluir uma rota. [Citação necessária]

Ao caminhar em grupos, a velocidade da pessoa mais lenta é calculada.

O governo de Naismith aparece na lei de estatutos do Reino Unido, embora não pelo nome. Os regulamentos de licenciamento de atividades de aventura se aplicam a fornecedores de várias atividades, incluindo trekking. Parte da definição de trekking é que ele está acima do terreno no qual levaria mais de 30 minutos para chegar a uma estrada ou refúgio (pela rota mais rápida e segura), com base em uma velocidade de caminhada de 5 quilômetros por hora mais um minuto adicional para A cada 10 metros de subida.

Um gráfico da velocidade de caminhada versus a inclinação resultante das correções da regra e do Langmuir da Naismith para velocidades básicas de 5 km/h e 4 km/h em comparação com a função de caminhada de Tobler.

Equivalência do lenço entre distância e escalada

Como alternativa, a regra pode ser usada para determinar a distância plana equivalente de uma rota. Isso é conseguido reconhecendo que o governo de Naismith implica uma equivalência entre distância e subida em termos de tempo: 3 milhas (= 15.840 pés) de distância é equivalente em termos de tempo a 2000 pés de escalada.

Professor Philip Scarf, reitor associado de pesquisa e inovação e professor de estatística aplicada na Universidade de Salford, em pesquisas publicadas em 2008, fornece a seguinte fórmula:

equivalent distance = x + α·y

Onde:

x = horizontal distancey = vertical distanceα = 7.92 (3 mi / 2000 ft ), called Naismith’s number by Scarf

Ou seja, 7,92 unidades de distância são equivalentes a 1 unidade de escalada. Por conveniência, uma regra de 8 a 1 pode ser usada. Assim, por exemplo, se uma rota é de 20 quilômetros (12 mi) com 1600 metros de escalada (como é o caso na perna 1 da rodada de Bob Graham, Keswick para Threlkeld), a distância plana equivalente desta rota é de 20+ ( 1,6 × 8) = 32,8 quilômetros (20,4 mi). Supondo que um indivíduo possa manter uma velocidade no apartamento de 5 km/h, a rota levará 6 horas e 34 minutos. A simplicidade dessa abordagem é que o tempo gasto pode ser facilmente ajustado para a velocidade (escolhida) de um indivíduo no apartamento; A 8 km/h (velocidade plana), a rota levará 4 horas e 6 minutos. A regra foi testada nos tempos de corrida de queda e considerada confiável. O lenço propôs essa equivalência em 1998.

Como você pode ver, a suposição do lenço permite também calcular o tempo para cada velocidade, não apenas um, como no caso da regra original da Naismith.

Ritmo

O ritmo é o recíproco da velocidade. Pode ser calculado aqui a partir da seguinte fórmula:

p = p0·(1 + α·m)

Onde:

p = pacep0 = pace on flat terrainm = gradient uphill

Esta fórmula é verdadeira para M≥0 (terreno subir ou plano). Assume equivalência de distância e escalada aplicando o fator α mencionado anteriormente.

Cálculos da amostra: P0 = 12 min / km (para 5 km / h de velocidade), M = 0,6 km de escalada / 5 km de distância = 0,12, p = 12, (1 + 7,92,0,12) = 23,4 min / km.

Outras modificações

Ao longo dos anos, vários ajustes foram formulados na tentativa de tornar a regra mais precisa, contabilizando variáveis adicionais, como carga transportada, rugosidade do terreno, descidas e aptidão (ou falta dela). A precisão de algumas correções é contestada, em particular a velocidade na qual os caminhantes descem um gradiente suave. Nenhuma fórmula simples pode abranger toda a diversidade de condições montanhosas e habilidades individuais.

Correções de Tranter

Esta seção não cita fontes. Ajude a melhorar esta seção adicionando citações a fontes confiáveis. Material não ouvido pode ser desafiado e removido. (Setembro de 2019) (Saiba como e quando remover esta mensagem de modelo)

As correções de Tranter fazem ajustes para fitness e fadiga. A aptidão é determinada pelo tempo que leva para subir 1000 pés a uma distância de 800 m (½ milha (800 m). Ajustes adicionais para terrenos ou condições irregulares ou instáveis podem ser estimados ao cair um ou mais níveis de condicionamento físico.

Individual fitness in minutesTime taken in hours estimated using Naismith's rule23456789101214161820222415 (very fit)11.522.753.54.55.56.757.751012.514.51719.52224201.252.253.254.55.56.57.758.751012.51517.52023251.534.255.578.51011.513.251517.53023.556.758.510.512.514.5402.754.255.757.59.511.5Too much to be attempted50 (unfit)3.254.756.58.5

Por exemplo, se a regra da NAMISMITH estima um tempo de viagem de 9 horas e seu nível de condicionamento físico for 25, você deve permitir 11,5 horas.

Correções de Aitken

Aitken (1977) assume que 1 h leva para cobrir 3 mi (5 km) em caminhos, faixas e estradas, enquanto isso é reduzido para 4 km (4 km) em todas as outras superfícies.

Para ambas as distâncias, ele fornece 1 h adicional por 2000 pés (600 m) de subida. Portanto, Aitken não leva em consideração a equivalência entre distância e escalada (proposta por lenço em 1998).

Correções de Langmuir

Langmuir (1984) estende a regra sobre a descida. Ele assume a velocidade básica do Naismith de 5 km/h e faz os seguintes refinamentos adicionais para descer ladeira abaixo:

For a gentle decline (slopes between 5 degrees and 12 degrees) subtract 10 minutes for every 300 meters of descent For a steep decline (slopes greater than 12 degrees) add 10 minutes for every 300 meters of descent

Mais tarde, ele diz, ou seja, que a aptidão do membro mais lento de uma parte deve ser levada em consideração e, portanto, mais prática para um grupo é a fórmula:

4 km/h + 1 h / 450 m of ascent

Veja também

Preferred walking speedTobler's hiking function